Лабораторная работа №6. Экспериментальное определение модуля упругости II рода (сдвига)
Цель работы – проверка справедливости закона Гука при кручении и определение модуля упругости II рода (модуля упругости при сдвиге).
Основные сведения
Экспериментальные исследования круглых стержней на кручение показывают, что в начальной стадии деформации происходит поворот одного сечения относительно другого на некоторый угол φ, называемый углом закручивания.
Для большинства металлов наблюдается линейная зависимость между углом закручивания φ и крутящим моментом Мк, т.е. соблюдается закон Гука:
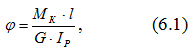
где l – расчетная длина образца;
G – модуль упругости II рода (модуль сдвига);
Iр – полярный момент инерции поперечного сечения стержня;
GIР – жесткость стержня при кручении.
Величина модуля G определяется экспериментально из опытов на кручение, хотя теоретически она не является независимой от других постоянных, характеризующих упругие свойства изотропных материалов: модуля упругости I рода Е и коэффициента Пуассона υ:
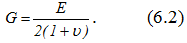
Порядок выполнения и отработка результатов
Испытания проводят с использованием машины МК-50 на стандартном образце d = 15 мм (ГОСТ 3565-80). Изменение угла закручивания образца определяют с помощью торсиметра.
Максимальное нагружение определяют по формуле
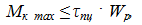
где τпц – предел пропорциональности при сдвиге;
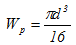
— полярный момент сопротивления поперечного сечения стержня.
Зная диапазон нагружения, определяют число замеров (5 или 6) и величину ступени нагружения ΔМк.
Ознакомившись с устройством торсиметра и испытательной машины МК-50, торсиметр настраивают таким образом, чтобы цена деления стрелочного индикатора соответствовала углу поворота на 1 мин.
Нагружение производится вручную.
Начальный крутящий момент Мк принимают за условный ноль и снимают первое показание по торсиметру. Далее увеличивают крутящий момент одинаковыми ступенями ΔМк, снимают показания на торсиметре и заносят их в журнал испытания. Доводят нагрузку до очередного значения плавно (для этого ручку нагружения держат двумя руками), не «перескакивая» нужное значение, т. к. даже частичная разгрузка недопустима.
Снятие отсчетов можно производить и при разгрузке, соблюдая сказанные правила, т.е. плавно, без «перескакивания». При получении адекватных значений результаты опыта можно считать достоверными.
В процессе испытания образца на кручение после каждой ступени нагружения регистрируют Мк [Н·м] и угол закручивания φ [мин], которые заносят в первые колонки журнала наблюдений, затем по этим данным строят график диаграммы закручивания образца в координатах Мк-φ, по которому проверяют линейную зависимость, т.е. справедливость закона Гука.
После очередной записи отсчетов моментов и углов закручивания в журнале испытаний для каждой ступени нагружения производят подсчет приращений показаний крутящего момента и угла закручивания, которые заносят во вторые колонки. Среднее приращение угла закручивания Δφср определяют по формуле
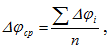
где n – число ступеней нагружения.
Тогда (используем формулу (6.1)) модуль упругости II рода будет равен
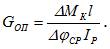
Полученные в опыте значения модуля упругости II рода сравнивают с табличным значением
Gт = 0,8 · 1011 Па и определяют погрешность опыта:
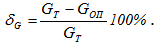
В заключение работы делают выводы.
Контрольные вопросы
- При каком нагружении прямой брус испытывает деформацию кручения?
- Какое правило знаков принято для крутящих моментов?
- Что называется углом закручивания?
- Как выражается закон Гука при кручении?
- По каким формулам можно определить модуль упругости второго рода?
- Как опытным путем определяется модуль упругости второго рода?
- Как экспериментально определяется угол закручивания образца? Какие измерительные приборы и приспособления при этом применяются?
- Что называется жесткостью поперечного сечения бруса при кручении? Размерность жесткости поперечного сечения.
- Какие факторы влияют на величину угла закручивания?
- По какой формуле определяется полярный момент сопротивления для круглого вала сплошного сечения и для вала кольцевого сечения?
Испытание материалов на срез >
Другие лабораторные работы >
Примеры решения задач >
