Пример решения задачи на расчет деформаций участков и изменение общей длины стального стержня при его растяжении-сжатии.

Задача

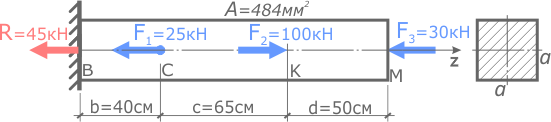
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.

Другие примеры решений >
Помощь с решением задач >

Модуль продольной упругости стали E=200ГПа.

Пример решения

Предыдущие пункты решения задачи

1. Определение опорных реакций,
2. Построение эпюр внутренних продольных сил,
3. Подбор размеров поперечного сечения стержня,
4. Построение эпюр нормальных напряжений.

Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.

Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:

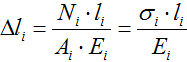
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.

Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).

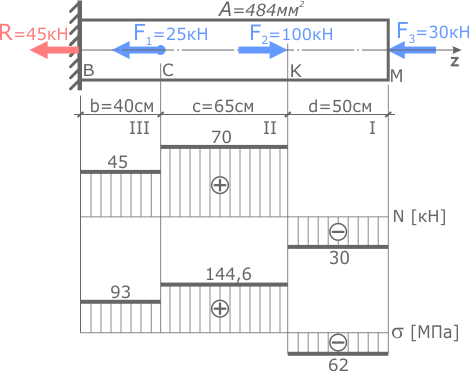
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).

Рассчитаем их:

Деформация I участка (KM)

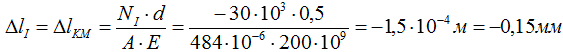
II участок (CK)

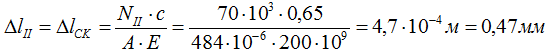
Удлинение третьего участка BC

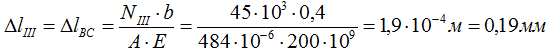
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:

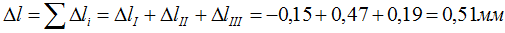
В результате деформации общая длина стержня увеличится на 0,51мм.

Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >