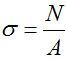Вывод формулы нормальных напряжений при растяжении-сжатии:
Если на прямой стержень до его нагружения нанести сетку из продольных и поперечных линий, то после его растяжения (сжатия) мы увидим, что эти линии остались параллельны своему первоначальному положению.
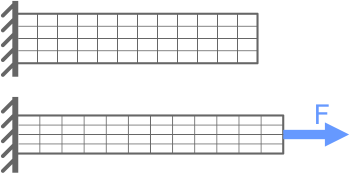
Это говорит о том, что при продольном нагружении, поперечные сечения бруса перемещаются поступательно.
В соответствии с гипотезой плоских сечений, можно утверждать, что при растяжении-сжатии напряжения во всех точках поперечного сечения одинаковы, т.е. σ=const.
Рассмотрим равновесие отсеченной части стержня.
Под действием внешней силы F в поперечном сечении возникает внутреннее усилие N,
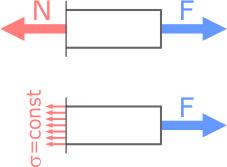
которое в свою очередь вызывает нормальные напряжения σ одинаковой величины в каждой точке сечения.
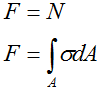
где A — площадь поперечного сечения стержня.
То есть внутренняя сила N равна сумме всех нормальных напряжений σ в сечении
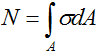
Учитывая, что нормальные напряжения постоянны (σ=const), вынесем их за знак интеграла
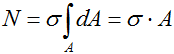
и получаем формулу для расчета нормальных напряжений при растяжении-сжатии.