Ответы на билеты экзамена по теоретической механике (два вопроса и три задачи) по разделам «Кинематика» и «Статика».
1. Способы задания движения точки.
Движение точки можно изучать, используя любую систему координат. Рассмотрим три способа задания движения: векторный, координатный и естественный.
Векторный способ
Будем рассматривать случай декартовой прямоугольной системы координат. Движение точки относительно рассматриваемой системы отсчета задано векторным способом, если известен радиус-вектор r этой точки как функция времени, т.е. r=r(t).
Векторный способ обычно применяется для теоретического изложения кинематики точки.
Координатный способ
Движение точки можно рассматривать в различных системах координат. Рассмотрим случай декартовой прямоугольной системы координат. Движение точки задано координатным способом, если известны координаты точки, как непрерывные, дважды дифференцируемые функции времени, т.е.
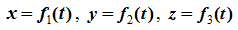
Уравнения движения есть также уравнения траектории точки в параметрической форме. Параметром является время t.
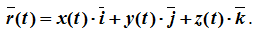
Уравнения траектории в координатной форме получаются из параметрических уравнений исключением параметра t. Получаются уравнения двух поверхностей Ф1(x,y)=0 и Ф2(x,y)=0. Пересечение этих поверхностей дает кривую в пространстве – траекторию точки.
Пример
Движение точки задано векторным уравнением
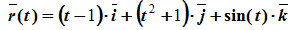
Это векторный способ задания движения.
Движение точки задано уравнениями
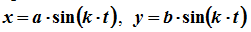
(a, b и k — постоянные величины). Это координатный способ задания движения.
Естественный способ задания движения
При естественном способе задания движения задаются траектория точки и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы отсчета.
Для задания закона движения точки по траектории необходимо выбрать на траектории точку О, принимаемую за начало отсчета и указать направление положительного отсчета.
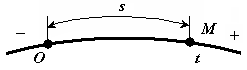
s=f(t) — закон движения точки по траектории. Величина s является расстоянием от начала отсчета до текущего положения точки, ее еще называют дуговой координатой. Функция s=f(t) должна быть непрерывной и дважды дифференцируемой.
Пример
Точка движется по окружности радиуса R в соответствии с законом s=t2-4, (s — в метрах, t — в секундах). Это естественный способ задания движения.
От задания движения в декартовых координатах можно перейти к его заданию естественным способом. Пусть движение задано координатным способом: x=f1(t), y=f2(t), z=f3(t). Дифференциал расстояния s выражается через декартовы координаты следующим образом
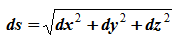
и после интегрирования по времени получаем
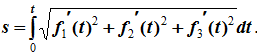
2. Центр параллельных сил
Рассмотрим систему параллельных сил {F1, F2, …, Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1, а). Эта точка называется центром параллельных сил.
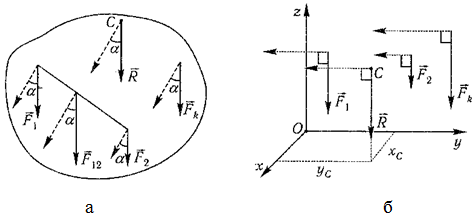
Для определения координат центра параллельных сил воспользуемся теоремой Вариньона о моменте равнодействующей относительно оси. Относительно оси x:
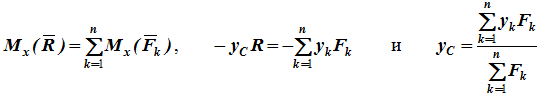
Относительно оси y:
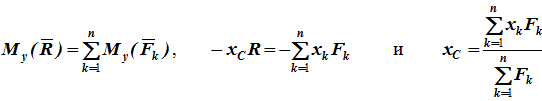
Чтобы определить координату zc повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок 1, б). Тогда
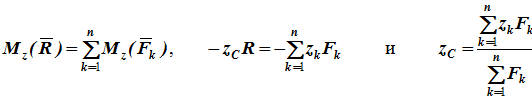
Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид
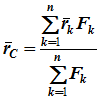
Свойства центра параллельных сил:
- сумма моментов всех сил Fk относительно точки C равна нулю ∑MC(Fk)=0;
- если все силы повернуть на некоторый угол α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой C.
Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 2).
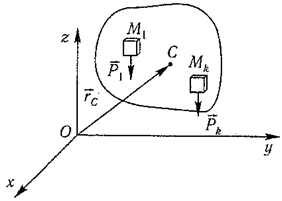
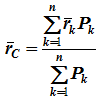
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
γ – удельный вес однородного тела, Pk=γΔVk, P=γV.
Подставив эти значения в формулу для определения rC, имеем
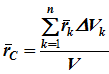
3. Решение задачи №1
Абсолютное ускорение равно
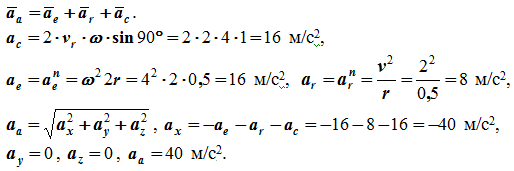
4. Решение задачи №2
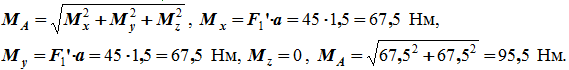
5. Решение задачи №3
Определим сумму моментов всех сил относительно точки A в случае равновесия системы:
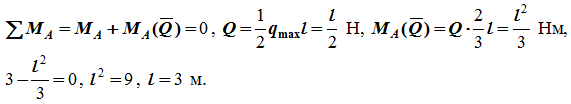
Ответы на другие экзаменационные билеты по теоретической механике можно найти на нашем сайте.
