Центром масс механической системы называется такая геометрическая точка C, концентрируя в которой (мысленно) массу M всей механической системы, получим, что ее статический момент массы равен статическому моменту массы всей механической системы, т.е.
Отсюда
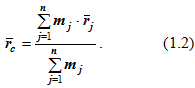
Проецируя обе части равенства (1.2) на оси координат, получаем аналитические формулы для координат центра масс механической системы:
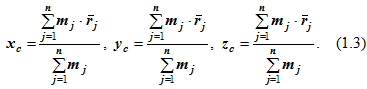
Выражению (1.2) можно придать и другой вид, если умножить числитель и знаменатель ее правой части на ускорение силы тяжести. В этом случае
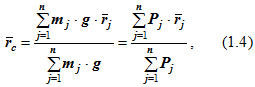
где Pj = mj ∙ g (j = 1,2,3,…,n) – веса материальных точек, образующих механическую систему;
∑Pj = M ∙ g = G – вес всей механической системы.
Выражение (1.4) определяет радиус-вектор центра тяжести неизменяемой материальной системы в предположении, что она находится в поле силы тяжести.
Отсюда следует, что центр тяжести неизменяемой (жесткой) механической системы (в частности твердого тела) совпадает с центром масс.
Однако понятия о центре масс и центре тяжести механической системы не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести.
Понятие же о центре масс как о характеристике распределения масс в механической системе является более широким, так как имеет смысл для любой механической системы независимо от того, находится ли данная система под действием каких-либо сил или нет. Поэтому понятие центра тяжести можно рассматривать как частный случай по отношению к понятию центра масс.
В общем случае следует говорить о центре масс материальной (механической) системы, а не о центре тяжести. При определении центра масс материальной системы можно пользоваться методами, установленными в статике для определения центра тяжести (метод симметрии, метод расчленения на простейшие элементы, метод отрицательных масс и т.д.).
