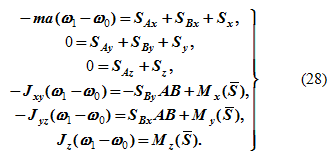Центральным ударом тела о неподвижную преграду называют удар, при котором нормаль к поверхности преграды в точке соприкосновения проходит через центр масс тела. В противном случае удар называется нецентральным.
При рассмотрении явления удара необходимо отказаться от понятия абсолютно твердого тела.
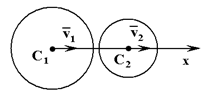
Рассмотрим прямой центральный удар двух тел, движущихся поступательно (рисунок 2): ν1,ν2 – скорости тел до удара, C1, C2 – центры масс тел.
Внешние ударные импульсы отсутствуют, поэтому для системы двух тел количество движения системы не изменяется
Коэффициент восстановления
Решая совместно эти два уравнения, находим:
u2 = ν2 + (1+k)(v1 — v2)m2 /(m1+m2) (16)
Если k = 0, то u1 = u2 = u. Отсюда скорость системы двух тел в конце неупругого удара
Для определения ударного импульса воспользуемся теоремой об изменении количества движения за время удара для одного из тел
Откуда:
При абсолютно упругом ударе ударный импульс в два раза больше, чем при абсолютно неупругом.
Из-за остаточных деформаций и нагревания тел при ударе происходит частичная потеря начальной кинетической энергии соударяющихся тел.
При прямом центральном ударе двух тел потерю кинетической энергии можно представить в виде теоремы Карно: кинетическая энергия, потерянная при прямом центральном не вполне упругом ударе двух тел, равна (1-k)/(1+k)-той части той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями
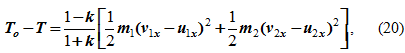
где m1 и m2 – массы соударяющихся тел, ν1x и ν2x – проекции скоростей соударяющихся тел на ось Ox до удара, u1x и u2x – проекции скоростей соударяющихся тел на ось Ox после удара.
Величины (ν1x — u1x) и (ν2x — u2x) называются потерянными скоростями и показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел.
Если при неупругом ударе (k = 1) одно из тел (например, второе) до удара находилось в покое, то
ν2 = 0,
T0 = ½m1v12,
T = ½(m1 + m2)u12 (21)
Формула (17) принимает вид
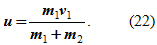
При этом
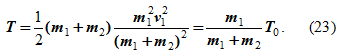
Потеря кинетической энергии при ударе
откуда
При действии ударного импульса на твердое тело, вращающееся вокруг неподвижной оси, для определения угловой скорости используется теорема об изменении кинетического момента (7) или
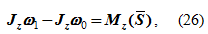
где Jz – момент инерции вращающегося тела,
Mz(S) – момент ударного импульса относительно оси вращения тела,
ω0, ω1 – угловая скорость вращающегося тела соответственно до и после действия ударных импульсов.
Отсюда угловая скорость тела
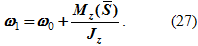
При действии ударного импульса на вращающееся тело угловая скорость изменяется на величину, равную отношению момента этого импульса относительно оси вращения к моменту инерции тела относительно той же оси.
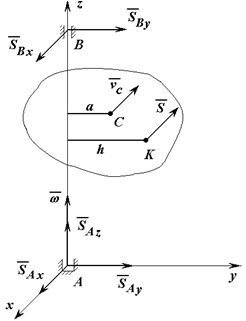
Для определения импульсов ударных реакций в подшипниках (рисунок 3) введем подвижную систему координат, проведя плоскость через центр масс, и воспользуемся теоремами об изменении количества движения (6) и об изменении кинетического момента (8). При этом:
ucx = -ωa; ucy = ucz = 0;
Lx(1) = -Jzxω0; Ly(1) = -Jyzω0; Lz(1) = Jzω0;
Lx(2) = -Jzxω; Ly(2)= -Jyzω; Lz(2) = Jzω;
здесь Jz – момент инерции тела относительно оси z, Jzx, Jyz – центробежные моменты инерции тела относительно осей z, x и осей y, z.
Получим шесть уравнений для определения импульсов ударных реакций и угловой скорости после удара: