Рассмотрим определение скорости и ускорения точек при естественном способе задания движения:
Из определения скорости точки
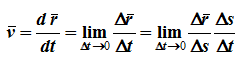
где
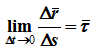
— единичный вектор касательной, тогда
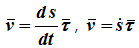
Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.
Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
Из определения ускорения точки
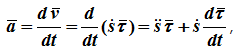
поскольку τ — переменный по направлению вектор, то:
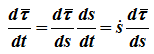
Производная
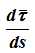
определяется только свойствами траектории в окрестности данной точки, при этом
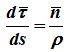
n — единичный вектор главной нормали,
ρ — радиус кривизны траектории в данной точке.
Таким образом,
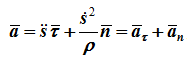
т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:
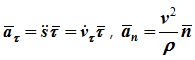
Здесь:
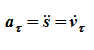
- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

- нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (ab=0).
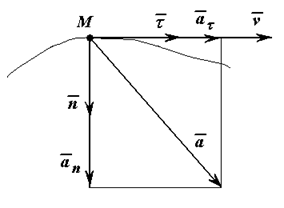
Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.
