Момент силы относительно точки (или центра) — вращательный эффект силы, характеризующий вращение твердого тела вокруг некоторой точки под действием приложенной силы.
Определение
Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
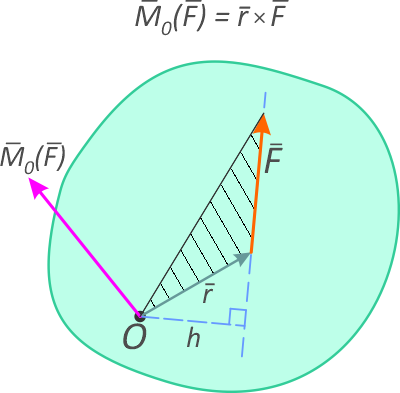
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
Вычисление момента
Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
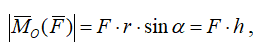
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.
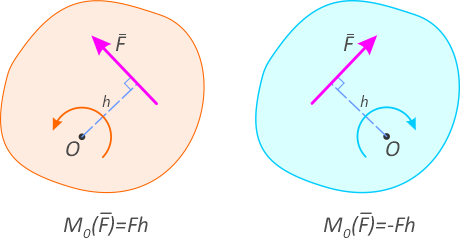
Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Наш короткий видеоурок про момент силы с примерами:
Правило знаков
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.
Если сила F задана своими проекциями на оси координат Fx, Fy, Fz и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:

Проекции момента силы на оси координат равны:

