Для расчета неизвестных сил в составных конструкциях необходимо разъединять соединенные элементы по шарнирным соединениям, заменяя воздействие отсоединенных частей реакциями связей.
Составными конструкциями или соединенными телами называют конструкции, состоящие из двух или более частей, соединенных между собой подвижным образом, например, шарниром (рисунок 1).
Для расчета неизвестных величин необходимо расчленять соединенные тела, вводя в рассмотрение реакции связей.
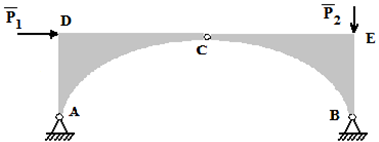
Освобождая конструкцию (рисунок 1), находящуюся под действием сил P1 и P2, от связей, получим четыре неизвестных величины XA, YA, XB, YB (рисунок 2).
Для произвольной плоской системы сил можно составить три уравнения равновесия. Значит, в таком виде задача не решается.
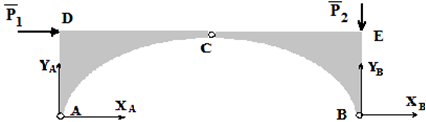
Выход находится, если расчленить конструкцию по подвижному соединению.
При отбрасывании правой части конструкции необходимо показать ее влияние на левую часть. Поскольку величина и направление силы, с которой правая часть действует на левую, неизвестны, вводим две ее составляющие XC, YC (рисунок 3).
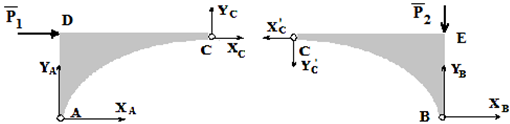
Если вся конструкция находится в равновесии, то и отдельные ее части должны находиться в равновесии. Теперь можно составить три уравнения равновесия для левой части конструкции и три уравнения равновесия для правой.
Согласно третьему закону Ньютона, с какой силой правая часть действует на левую, с такой же по величине и противоположной по направлению силой левая часть действует на правую (XC = X’C, XC = -X’C, YC = Y’C, YC = -Y’C).
Составим уравнения равновесия для левой части конструкции:
Для правой части конструкции:
Решив систему из шести уравнений, найдем неизвестные реакции, а также реакции XA, YA, XB, YB, возникающие в подвижном соединении C — XC, YC.
Другим способом решения такой задачи является аналогичное составление уравнений равновесия для целой конструкции и одной ее части.
Для системы из N тел в случае, когда на каждое тело действует произвольная плоская система сил, можно составить 3N уравнений равновесия и определить 3N неизвестных.
