Теорема гласит: изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.

Рассмотрим движение произвольной точки системы из первого положения во второе:

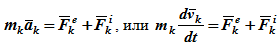
где F_k^e — внешние силы, действующие на систему,
F_kⁱ — внутренние силы системы.

Умножим обе части уравнения скалярно на дифференциал радиуса-вектора dr_k тогда

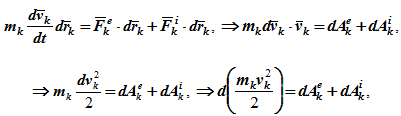
где T_k — кинетическая энергия точки;

далее получим

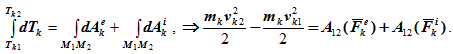
Просуммируем по всем точкам системы

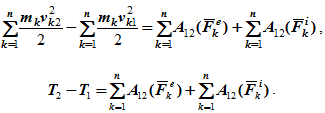
То есть, изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.

Если в формуле (1.1) обе части уравнения разделить на dt, то можно записать теорему об изменении кинетической энергии системы в дифференциальной форме: производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил, действующих на систему.

Суммируя по всем точкам системы, получим

Примеры решения задач >
Закон сохранения механической энергии >