Теорема о трех моментах гласит: при равновесии произвольной плоской системы сил алгебраическая сумма моментов сил относительно трех произвольных точек A, B и C, не лежащих на одной прямой, равна нулю, т.е.

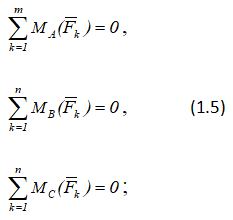
Это вторая форма условий равновесия произвольной плоской системы сил.

Необходимость этих условий очевидна, т.к. если плоская система сил находится в равновесии, то выполняется первая форма условий равновесия (4).

А тогда из последнего равенства (4) следует, что сумма моментов всех сил относительно любой точки, следовательно, и точек A, B, C равняется нулю, т.е. выполняются условия (1.5).

Достаточность условий (1.5) следует из того, что если эти условия выполняются, а данная система сил не находится в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки A, B и C.

Но это невозможно, т.к. точки A, B, C не лежат на одной прямой. Следовательно, если выполняются условия (1.5), то имеет место статическое равновесие.

Далее: