Рассмотрим примеры определения мгновенного центра ускорений (МЦУ) для некоторых частных случаев:
В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нулю.
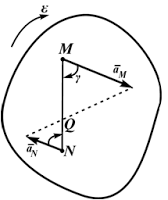
Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать её буквой Q
Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:
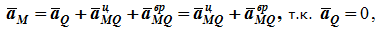
или
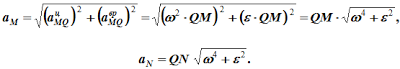
Угол, который составляет вектор ускорения точки M с линией MQ, определится из соотношения:
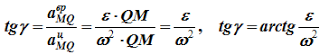
То есть у всех точек плоской фигуры этот угол одинаков.
Из рисунка 2.23 видно, что мгновенный центр ускорений лежит в точке пересечения линий, составляющих угол γ с соответствующими ускорениями точек.
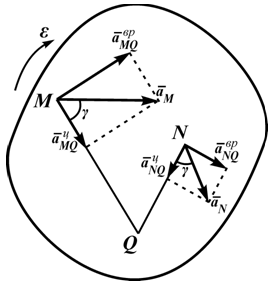
Рисунок 2.23
На рисунках 2.24 — 2.26 приведены частные случаи определения положения мгновенного центра ускорений.
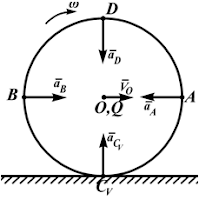
tqγ=0, γ=0,
aA=aB=aD=aCv=ω2R=V02/R,
т. O — МЦУ
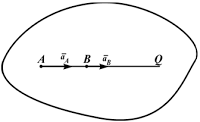
tqγ= ε/ω2=0,
γ=0o,
aA= ω2∙AQ,
aB= ω2∙BQ
Рисунок 2.24
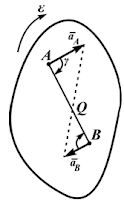
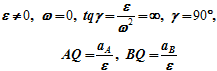
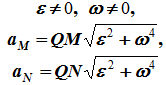
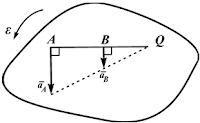
γ=90o,
aA=ε∙AQ, aB=ε∙AQ
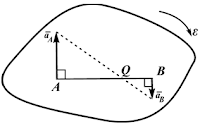
γ=90o,
aA=ε∙AQ, aB=ε∙AQ
Рисунок 2.26
