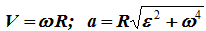Рассмотрим определение скоростей и ускорений точек вращающегося твердого тела:
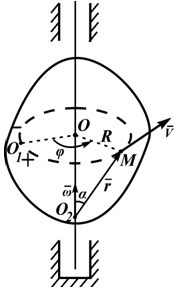
При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности R равен расстоянию от точки до оси вращения.
Закон движения точки может быть задан естественным способом (рисунок 2.4): траектория – окружность; начало отсчета точка O1 и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле
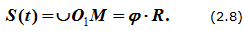
Скорости точек
Скорость точки вращающегося твердого тела определяется выражением
где ω — угловая скорость вращения твердого тела.
Скорость направлена по касательной к траектории, поэтому можно написать
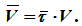
Вектор скорости можно получить векторным произведением:
V=ω × r × sinα=ω×R.
Ускорения точек
Ускорение точки при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):
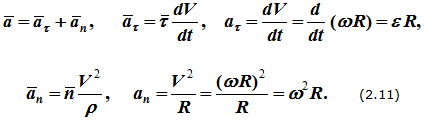
Эти же выражения можно получить, взяв производную от векторного произведения V=ω × r.
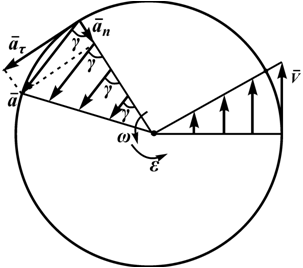
Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5)
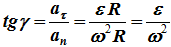
То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам: