Пример решения задачи по определению ускорения твердого тела, расположенного на гладкой горизонтальной поверхности, по грани которого, без скольжения, катится однородный круглый цилиндр заданной массы.
Задача
На гладкой горизонтальной поверхности помещена треугольная призма A массой m1. По грани призмы A, составляющей угол α с горизонтом, катится без скольжения однородный круглый цилиндр B массой m2.
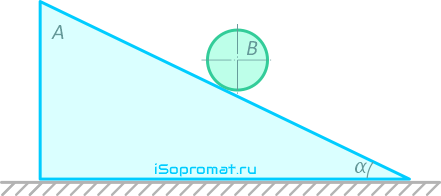
Требуется определить ускорение тела призмы.
Решение
Система имеет две степени свободы, ее положение определим обобщенными координатами q1 и q2 (рисунок 3.8), соответственно ускорения центров масс этих тел будут:
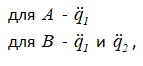
т.к. твердое тело B совершает сложное движение.
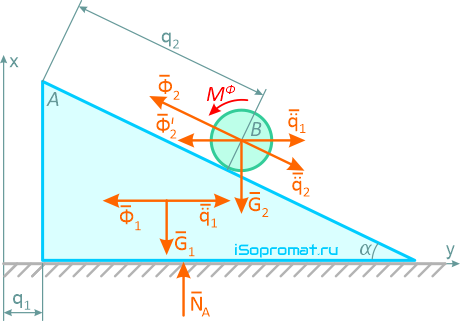
Покажем внешние действующие силы: G1, G2, NA. Силы инерции для тела A, движущегося поступательно, приводятся к вектору
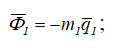
для твердого тела B, участвующего в сложном движении (переносное вместе с призмой и качение по призме A), силы инерции приводятся к
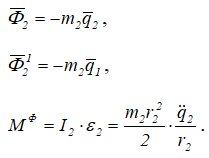
Зададим приращение координатам q1 и q2 соответственно δq1 и δq2. Приложенные внешние силы и силы инерции совершат работу
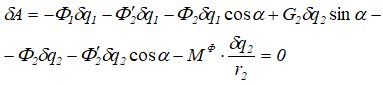
Составим общее уравнение динамики в обобщенных силах:
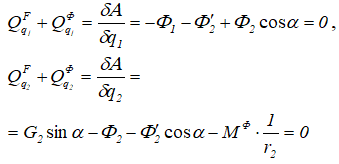
Подставляя заданные величины, получим
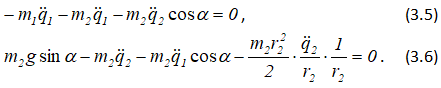
Из (3.5)
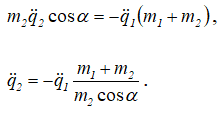
Подставляя в (3.6), получим
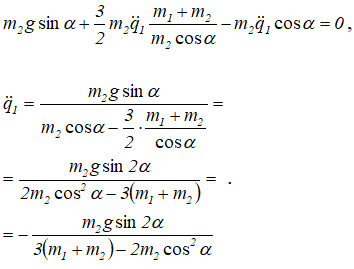
Задача решена.
Далее:
