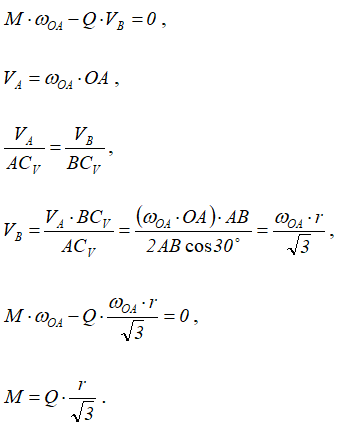Пример решения задачи по определению величины и направления момента M, уравновешивающего силу Q в плоском механизме с использованием принципа возможных перемещений.

Задача

Для механизма, представленного на рисунке 2.1, определить величину момента M, уравновешивающего силу Q.

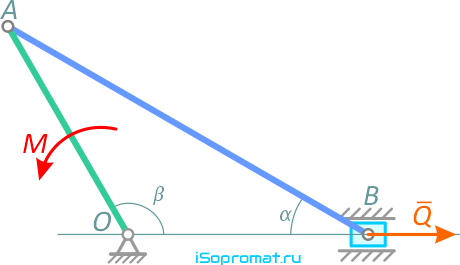
Дано: Q, α = 30°, β = 120°, OA = r.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Составим уравнение работ, выражающее принцип возможных перемещений. В данном случае связи идеальны: реакции опоры и реакция стенки цилиндра (гладкая) работу не совершают.

Определим зависимость между углом порота кривошипа OA и перемещением ползуна B.

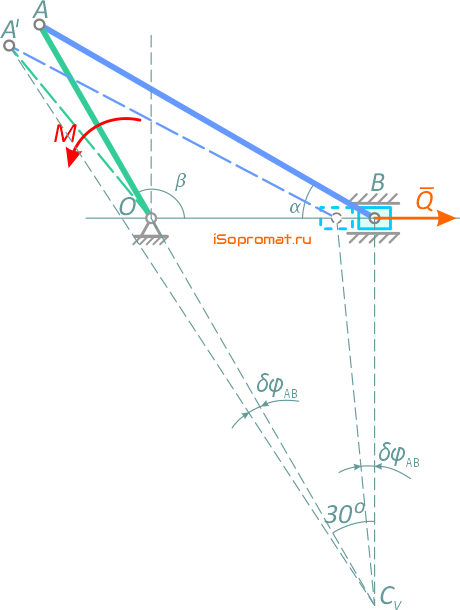
Примем за возможное перемещение кривошипа — δφ_OA.

Получим

шатун AB совершает плоское движение. В данный момент времени точка C_V — мгновенный центр вращения для шатуна AB, поэтому

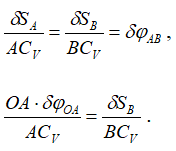
Из треугольника ABC_V:

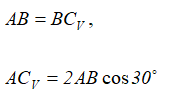
Находим зависимость между δφ_OA и δS_B:

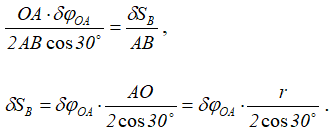
Определяем зависимость между моментом M и силой Q.

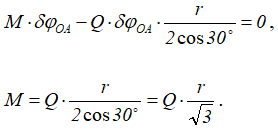
Такой же результат мы могли бы получить, если бы воспользовались соотношением (2.2), т.е. уравнением мощностей.

Другие примеры решения задач >