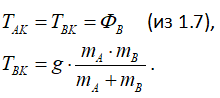Пример решения задачи по определению реакции гладкой горизонтальной поверхности, удерживающей тело, и реакции уступа, а также силы натяжения нити при движении груза.
Задача
По гладкой горизонтальной поверхности тела D (рисунок 1.1), может скользить тело B. К нему привязана невесомая нерастяжимая нить, она перекинута через невесомый блок K, и к концу нити привязан груз A.
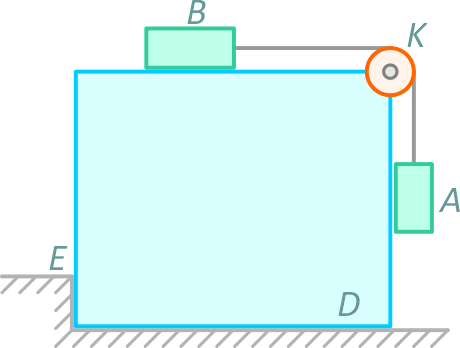
Дано: mD — масса тела D, mA, mB — массы тел A и B.
При движении груза A вниз определить реакцию гладкой горизонтальной поверхности, удерживающей тело D, и реакцию уступа E, а также силу натяжения нити.
Другие примеры решений >
Помощь с решением задач >
Пример решения
При решении задачи с помощью принципа Даламбера нужно указать все внешние действующие силы, реакции связей, силы инерции (рисунок 1.2).
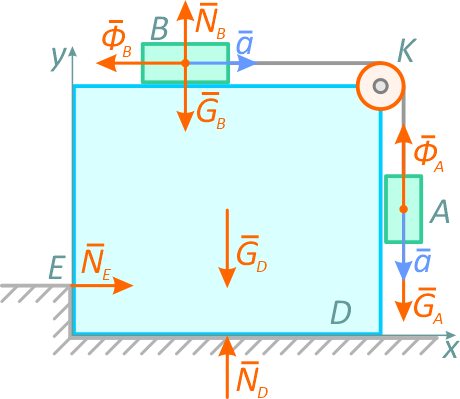
Геометрическая сумма этих сил должна быть равна нулю:
![]()
Спроецируем выражение (1.3) на выбранные оси координат:
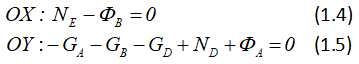
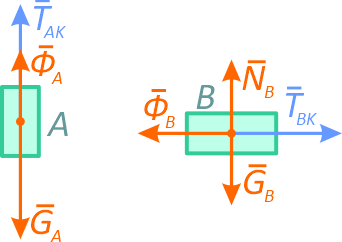
Для определения ускорения применим принцип Даламбера отдельно для груза A и груза B (рисунок 1.3). Запишем уравнения для грузов A и B в проекции на соответствующие оси:
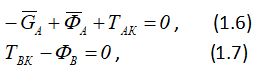
TAK, TBK — натяжение нити, для отдельно рассматриваемых груза A и B стало внешней силой.
Поскольку блок K невесомый, то
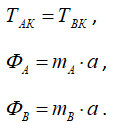
Подставляя (1.7) в (1.6), получим
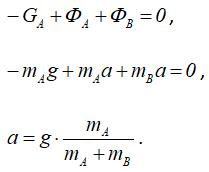
Подставляя значение ускорения в формулы (1.4) и (1.5), получим
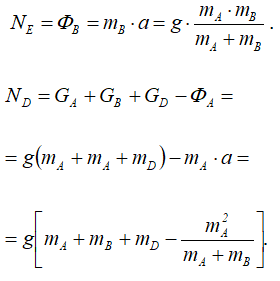
Определив ускорение, можно найти и натяжение нитей: