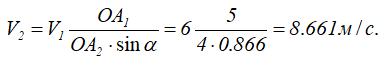Пример решения задачи по разделу «динамика» на определение скорости материальной точки в заданном положении, движущейся под действием центральной силы F.
Задача
Материальная точка движется в вертикальной плоскости zOy под действием центральной силы F, линия действия которой проходит через точку O.
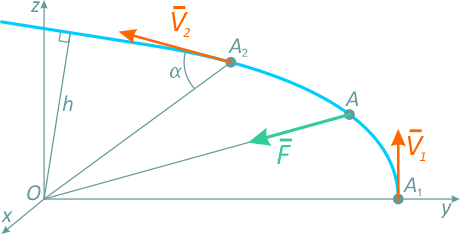
Найти скорость точки в положении A2, если в положении A1 ее скорость V1 равнялась 6м/с, причем OA1/OA2=5/4 и угол, образуемый скоростью V2 с линией действия силы, равен 60° (рисунок 3.5).
Другие примеры решений >
Помощь с решением задач >
Пример решения
К решению задачи применим теорему об изменении момента количества движения материальной точки относительно оси x, проходящей через точку O перпендикулярно плоскости рисунка:
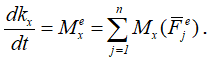
Так как к материальной точке приложена только центральная сила F, момент которой относительно оси x равен нулю, т.е.
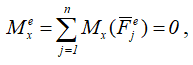
то kx=const и kx1=kx2, где kx1 и kx2 — моменты количества движения точки соответственно в точках 1 и 2.
Момент количества движения материальной точки в положении A1 относительно оси x
![]()
Момент количества движения точки в положении A2 относительно оси x
![]()
Тогда
![]()
откуда