Пример решения задачи по определению реакций в опорных точках системы трёх невесомых стержней, шарнирно скрепленных между собой и нагруженных силой.
Задача
Груз Q весом 1000Н подвешен в точке D, удерживаемой тремя невесомыми стержнями, шарнирно скрепленными между собой в точке D и с горизонтальной поверхностью в точках A, B и C (рисунок 2.4).
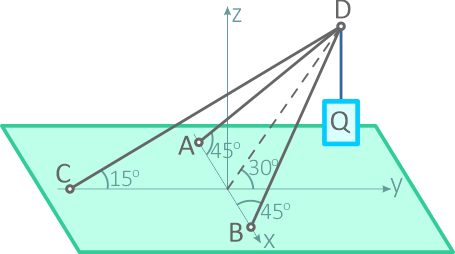
Определить реакции опор в точках A, B и C.
Другие примеры решений >
Помощь с решением задач >
Решение
В данной задаче следует рассмотреть равновесие точки D. Именно в этой точке пересекаются линии действия всех сил: натяжение троса Q, усилия в стержнях AD, BD, CD (рисунок 2.5).
Короткое видео про реакции в разных типах связей:
Силы направляем от узла D, тем самым предполагая стержни растянутыми. Это задача на равновесие пространственной системы сходящихся сил.
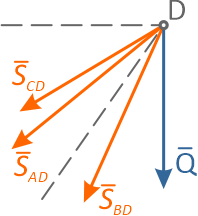
Геометрическое решение в данном случае не дает наглядного представления о геометрической сумме сил:
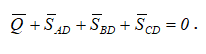
Поэтому векторное равенство проецируем на оси координат (рисунки 2.4, 2.5) и получаем три уравнения равновесия:
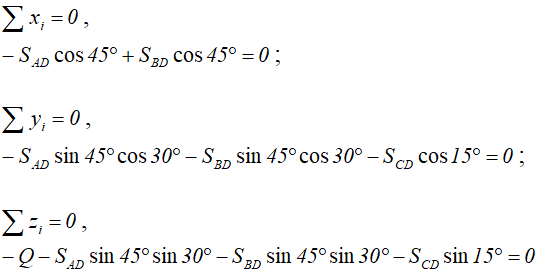
Решая полученные уравнения, определяем усилия в стержнях.
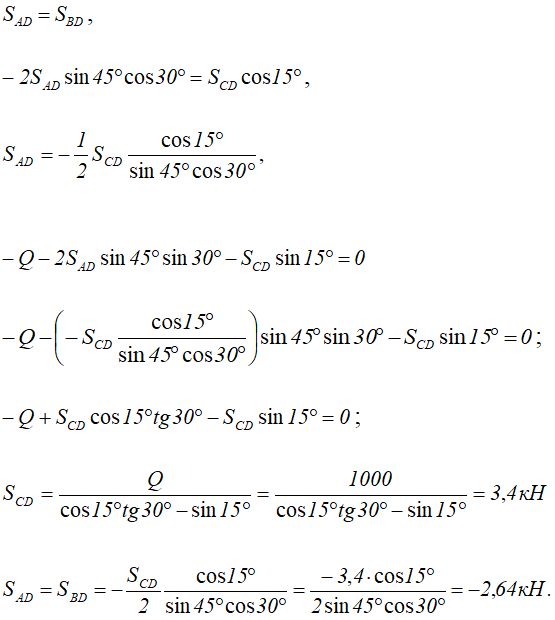
Стержень CD работает на растяжение, а стержни AD и BD сжаты. Соответственно реакции опор в точках A, B и C направлены вдоль стержней.
