Пример решения задачи по определению скоростей и ускорений точек штока для заданного положения кривошипного механизма.

Задача

Для данного положения механизма, изображенного на рисунке 2.26, требуется определить скорости и ускорения точек B и K.

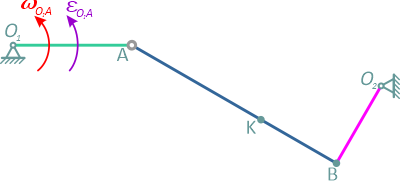
Дано: расстояния O₁A=20 см, АВ=40 см, О₂В=15 см, АК=25 см, и углы ∠О₁АВ=150°, ∠О₂ВА=90°.

Кривошип O₁A в данный момент вращается с угловой скоростью ω_О1А=2 с^-1 и угловым ускорением ε_О1А=2 с^-2 (против хода часовой стрелки).

Решение

В данном механизме точки А и B могут перемещаться по дугам окружностей с радиусами O₁A и О₂В соответственно, шток АВ совершает плоскопараллельное движение.

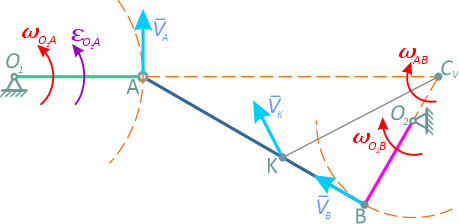
Определим скорость точки А:

Скорость точки А перпендикулярна отрезку O₁A и направлена вверх. Скорость точки B, как точки, вращающейся вокруг точки О₂, перпендикулярна О₂В, в нашем случае направлена вдоль линии АB.

Определим скорости точек B и K разными способами:

1) По теореме о скоростях точек в плоскопараллельном движении можно написать:

Точка A выбрана за полюс, т.к. о ней все известно. Направления линий, вдоль которых направлены V_B и V_BA, также известны.

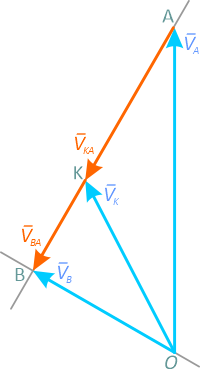
Строим по соответствующий формуле (2.17) треугольник (рисунок 2.28). Из произвольной точки в масштабе откладываем вектор V_A с соответствующим направлением.

Из конца вектора V_A проводим линию, перпендикулярную линии, проходящей через шток АB. Часть этой линии будет соответствовать вращательной скорости точки B вокруг полюса А.

Длину вектора V_BA получим, если из точки O проведем линию, параллельную скорости точки B.

Получившийся в результате такого построения треугольник соответствует формуле (2.17). Величины векторов V_B и V_BA можно получить, умножив длины стрелок на масштаб.

Если построение выполнялось не в масштабе, а лишь с соблюдением геометрии, то можно воспользоваться теоремой синусов:

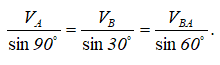
Из этого соотношения определяются величины V_B и V_BA соответственно:

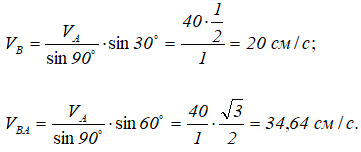
Определив скорость точки B во вращательном движении вокруг точки А (V_BA), можно определить угловую скорость штока АB:

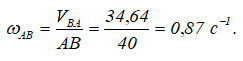
Направление вектора V_BA показывает, что вращение точки B вокруг точки А и, соответственно, штока АB происходит в направлении хода часовой стрелки (рисунки 2.27, 2.28).

Для определения скорости точки K можно написать

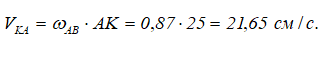
Этот вектор также как и V_BA перпендикулярен линии, проходящей через точки А и B, и на рисунке 2.28 он будет отложен по вектору V_BA. Можно написать соотношение:

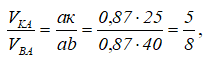
которое определяет положение точки K на линии AB и тем самым определяет величину и направление вектора V_K (рисунок 2.28):

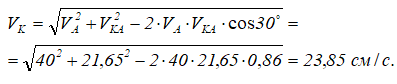
2) Скорость точки B может быть определена другим способом: с помощью следствия из теоремы о скоростях точек в плоскопараллельном движении (см. раздел 2.3.1.2).

Для данной задачи это следствие запишется

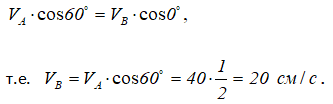
3) На практике более распространен способ определения скоростей точек в плоскопараллельном движении с помощью мгновенного центра скоростей (МЦС). Он находится в точке пересечения перпендикуляров к скоростям точек движущегося тела и для шатуна может быть записано соотношение (рисунок 2.27):

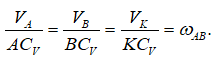
Так как геометрия механизма известна, то все расстояния и величины скоростей определяются:

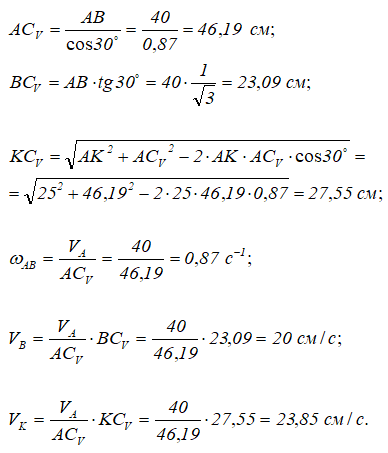
Определив скорость точки B, которая принадлежит и штоку AB и звену О₂В, можно найти угловую скорость О₂В:

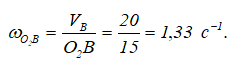
Для определения ускорений точек B и K определим ускорение точки A, вращающейся вокруг неподвижного центра О₁:

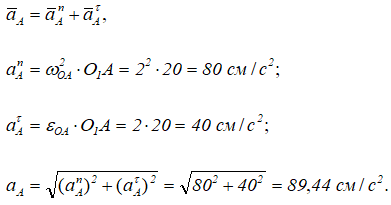
Приняв точку A за полюс запишем

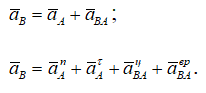
В последней формуле первые два слагаемых известны, а третье можно определить:

Этот вектор направлен от точки B к полюсу A.

Вращательное ускорение точки B вокруг A — a_BA^вр — по величине не определяется, но известно его направление:

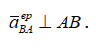
Учитывая, что точка B принадлежит двум звеньям и что звено О₂В вращается вокруг неподвижной точки О₂, можно написать формулу

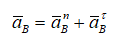
и, следовательно,

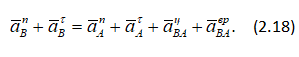
В формуле (2.18) a_Bⁿ — нормальное ускорение точки B при вращении вокруг О₂ известно:

Этот вектор направлен от точки B к точке О₂. Вектор a_B^τ известен только по направлению:

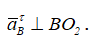
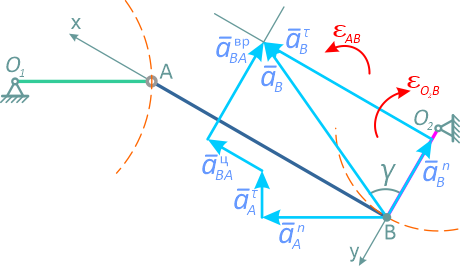
В формуле (2.18) две неизвестные по модулю величины. Эту векторную сумму можно построить (рисунок 2.29).

Пересечение линии, проведенной из конца вектора a_BA^ц перпендикулярно AB (по направлению вектора a_BA^вр) и линии, проведенной из конца вектора a_Bⁿ перпендикулярно BО₂ (так направлен вектор a_B^τ) определяют вектор a_B, так как это построение отражает формулы:

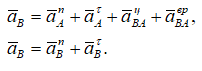
Если данное построение выполнялось с соблюдением масштаба, то измерив длины соответствующих отрезков, можно определить по величине a_B, a_B^τ, a_BA^вр.

Аналитическое определение величин этих векторов можно выполнить, спроецировав формулу (2.18) на выбранные оси координат (xBy). Расчет упрощается, если одну из осей совместить со штоком AB (рисунок 2.29):

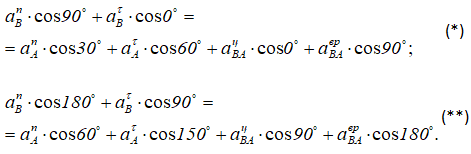
Из этих двух выражений определяются величины a_B^τ и a_BA^вp.

Из (*) и (**) следует:

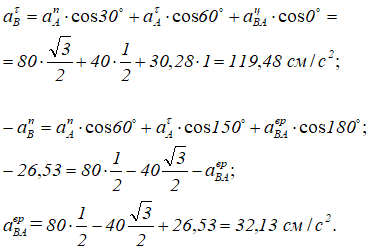
Определение этого вектора позволяет найти угловое ускорение штока AB:

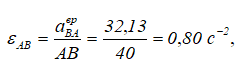
т.е. шток AB ускоряется против хода часовой стрелки, его вращение в данный момент замедленное. Определение a_B^τ дает возможность найти угловое ускорение звена BО₂:

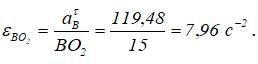
Звено BО₂ вращается ускоренно (направления ω_BO2 и ε_BO2 совпадают).

Полное ускорение точки B

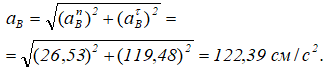
Вектор a_B составляет угол γ с звеном BО₂:

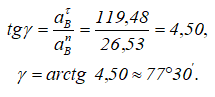
Ускорение точки K находится из формулы:

в которой все слагаемые определяются: a_Aⁿ и a_A^τ уже найдены:

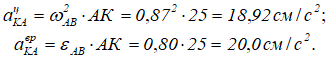
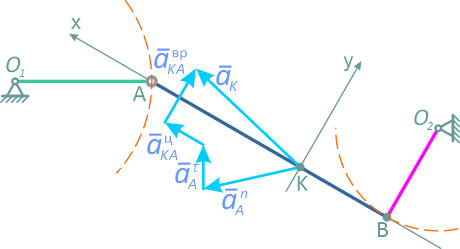
Спроецировав формулу (***) на оси системы xKy, получим:

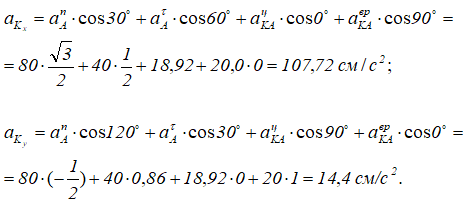
Полное ускорение точки K:

Определение угловой скорости и вращательного ускорения штока AB позволяют найти его мгновенный центр ускорений. Для этого определим угол β:

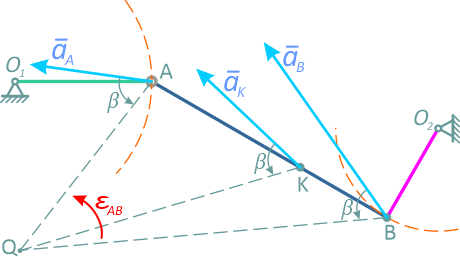
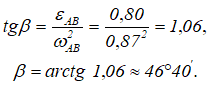
Отложив от известных ускорений точек A и B угол β («в сторону ε»), получим точку пересечения этих лучей Q (рисунок 2.31), которая и является мгновенным центром ускорений штока AB.

Ускорения точек должны соответствовать соотношениям:

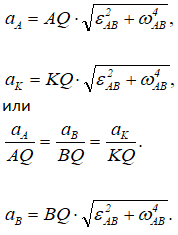
Задача решена.

---

Дополнительно: