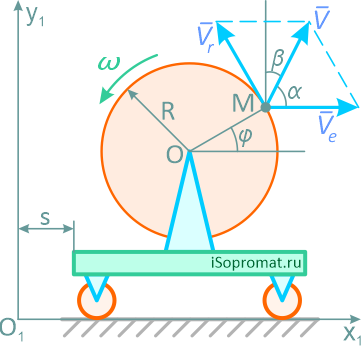
Пример решения задачи по определению в заданный момент времени и в заданном положении скорости и ускорения точки диска, расположенного на платформе, движущейся по горизонтальным направляющим.
Задача
Платформа движется по горизонтальным направляющим по закону s=2t2 м. На платформе установлен диск радиуса R=0,75 м, вращающийся вокруг оси перпендикулярной плоскости чертежа с угловой скоростью ω=4t2 рад/с.
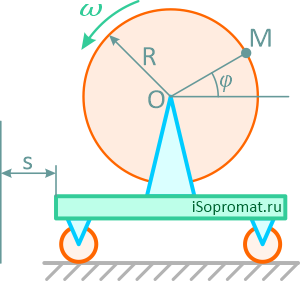
В момент времени t=2 с определить скорость и ускорение точки M, находящейся в положении, показанном на рисунке 3.8, φ=30°.
Другие примеры решений >
Помощь с решением задач >
Решение
В данном примере можно ввести неподвижную систему отсчета x1O1y1 и подвижную xOy, скрепленную с платформой.
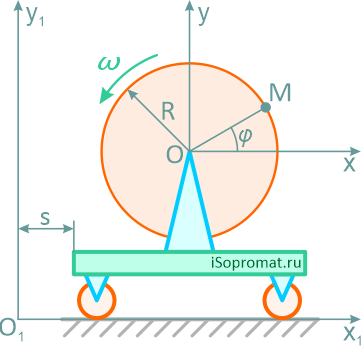
Подвижная система отсчета движется поступательно вместе с платформой. По отношению к подвижной системе отсчета движется диск (вращается вместе с точкой M вокруг оси, проходящей через точку O).
Движение точки подвижной системы отсчета, с которой в данный момент совпадает точка M, является переносным движением, вращение точки M вокруг точки O — относительное движение.
Скорость точки M определится по формулам:
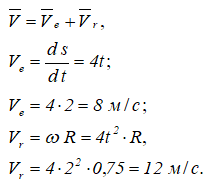
Спроецировав векторное равенство на оси неподвижной системы отсчета можно определить проекции абсолютной скорости на оси, величину скорости, направляющие косинусы.
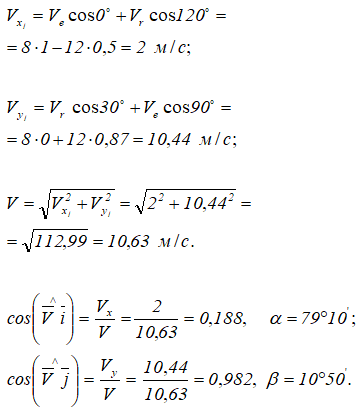
На рисунке 3.9 показаны переносная, относительная, абсолютная скорости точки M и углы, которые составляет вектор скорости с осями координат.
Ускорение точки определяется по формулам:
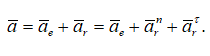
В данном примере при переносном поступательном движении (ωe=0) кориолисово ускорение равно нулю.
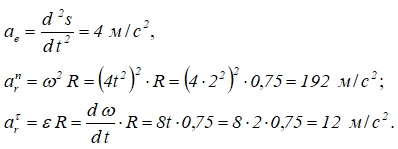
Проекции вектора абсолютного ускорения на оси:
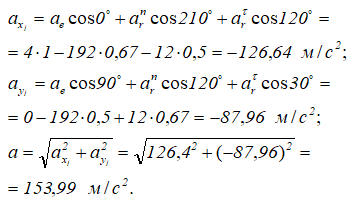
Направление вектора ускорения:
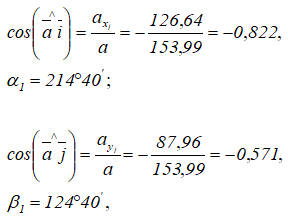
где α1 и β1 — углы, которые вектор ускорения составляет с осями координат.
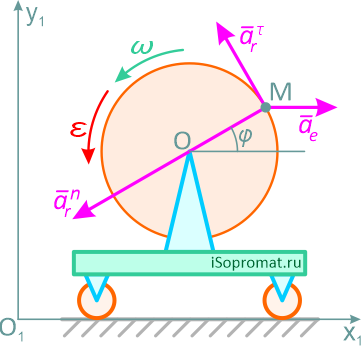
На рисунке 3.10 показаны составляющие полного ускорения точки M.
