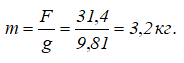Пример решения задачи по расчету величины максимальной массы груза F, до которой тело, лежащее на шероховатой горизонтальной поверхности, будет оставаться неподвижным (в равновесии).
Задача
Тело A массой m = 8 кг поставлено на шероховатую горизонтальную поверхность стола. К телу привязана нить, перекинутая через блок B (рисунок 25).
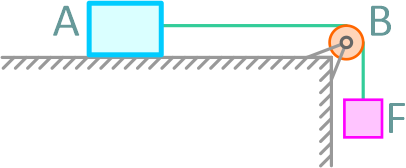
Требуется определить, какой груз F можно подвязать к концу нити, свешивающейся с блока, чтобы не нарушить равновесия тела A?
Коэффициент трения f = 0,4; трением на блоке пренебречь.
Решение
Определим вес тела A:
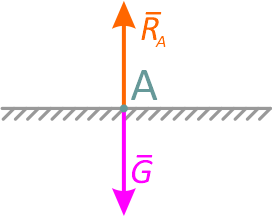
Считаем, что все силы приложены к телу A.
Когда тело поставлено на горизонтальную поверхность, то на него действуют только две силы: вес G и противоположно направленная реакция опоры RA (рисунок 26).
Если же приложить некоторую силу F, действующую вдоль горизонтальной поверхности, то реакция RA, уравновешивающая силы G и F, начнет отклоняться от вертикали, но тело A будет находиться в равновесии до тех пор, пока модуль силы F не превысит максимального значения силы трения Rf max, соответствующей предельному значению угла φ0 (рисунок 27).
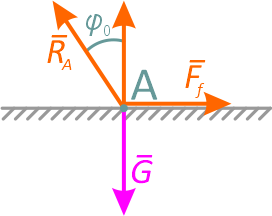
Разложив реакцию RA на две составляющие Rf max и Rn, получаем систему четырех сил, приложенных к одной точке (рисунок 28).
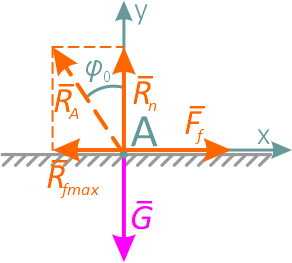
Спроецировав эту систему сил на оси x и y, получим два уравнения равновесия:
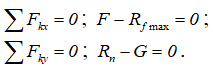
Решаем полученную систему уравнений: F = Rf max, но Rf max = f×Rn, а Rn = G, поэтому
Таким образом, тело A останется неподвижным при условии, что к концу нити, перекинутой через блок, подвешен груз, не превышающий по весу 31,4 Н.
При этом масса груза F
Далее:
