Пример решения задачи по определению координат положения центра тяжести объемного тела сложной формы по заданным размерам.
Задача
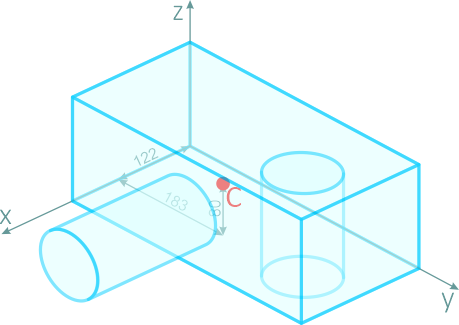
Определить положение центра тяжести тела, форма и размеры которого показаны на рисунке 2.7 (размеры указаны в мм)
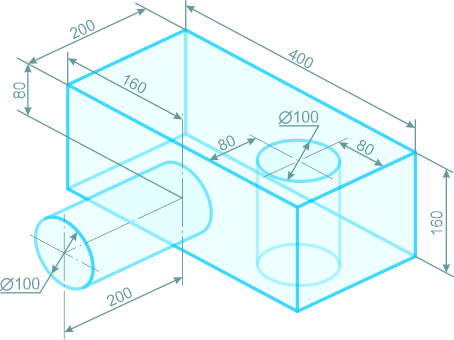
Рисунок 2.7
Другие примеры решений >
Помощь с решением задач >
Решение
Тело состоит из прямоугольного параллелепипеда 1 с центром тяжести C1, цилиндра 2 (C2) и цилиндра 3 (C3), объем которого считаем отрицательным.
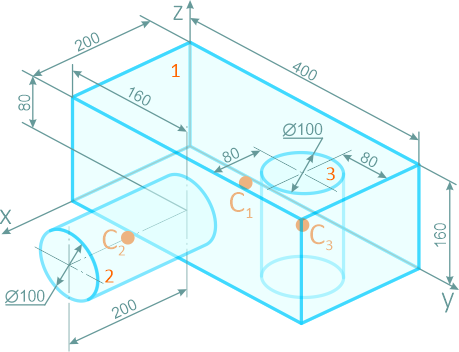
Найдем объемы составных частей и координаты xk , yk , zk их центров тяжести (в см):
V1= 12800 см3; C1 (10; 20; 8);
V2= 1570 см3; C2 (30; 16; 8);
V3= -1256 см3; C3 (12; 32; 8).
V2= 1570 см3; C2 (30; 16; 8);
V3= -1256 см3; C3 (12; 32; 8).
Определим координаты центра тяжести тела:
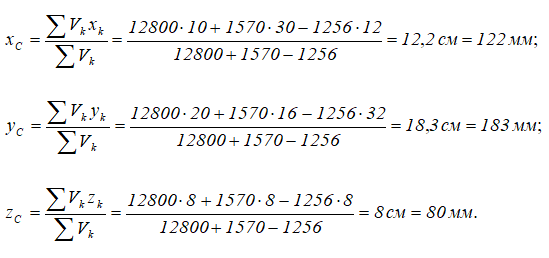
Таким образом, центр тяжести данного тела находится в точке C с координатами (122;183;80).