Пример решения задачи по определению величины груза Q, при котором вал останется в равновесии, и реакций подшипников A и B.
Задача
На вал ворота 1 намотана веревка, удерживающая груз весом Q (рисунок 23). Радиус колеса 2 ворота в четыре раза больше радиуса вала.
Веревка, прикрепленная к ободу колеса и натягиваемая грузом силой F = 80 Н, сходит с колеса в точке K по касательной. Радиус DK колеса образует с вертикалью угол α = 60°.
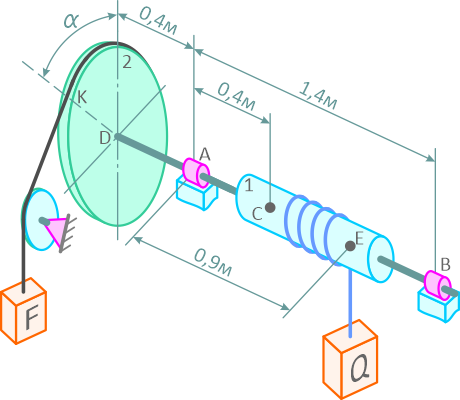
Требуется определить величину груза Q, при котором ворот остается в равновесии, а также реакции подшипников A и B, если общий вес вала и колеса G = 600 Н и приложен в точке C (AC = 0,4 м).
Решение
Три нагрузки – вес G и грузы Q и F, приложенные к вороту, уравновешиваются реакциями подшипников A и B, т.е. на вал действует произвольная пространственная система сил.
Короткое видео про реакции в разных типах связей:
Нагрузки действуют в плоскостях, перпендикулярных к оси вала, и, следовательно, не смещают вал вдоль оси, поэтому реакции подшипников действуют в плоскостях, перпендикулярных к этой же оси.
Заменим их составляющими проекциями RAx, RAy, RBx и RBy.
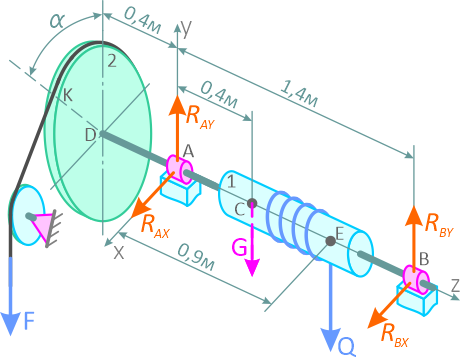
Заметим, что обычный подшипник не создает реакции, направленной вдоль оси вала. Если на вал действуют нагрузки, смещающие вал вдоль оси, то один из подшипников должен быть заменен подпятником.
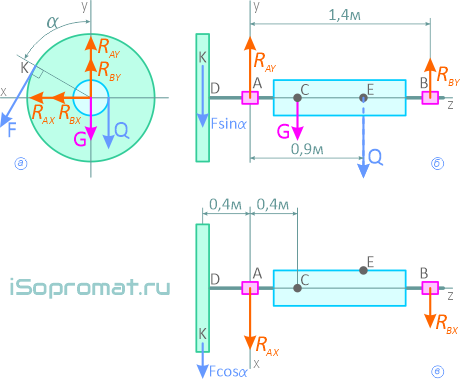
На рисунке 25 изображен вал со всеми действующими на него силами в трех проекциях (а, б и в).
Составим уравнения равновесия:
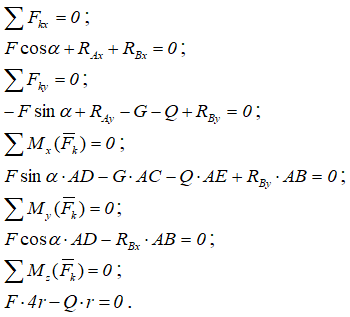
Решив уравнения, получим
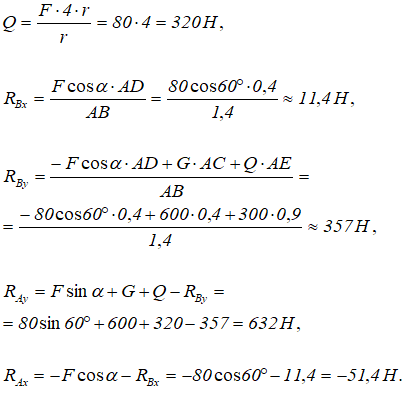
Отрицательное значение реакции RAx означает то, что она направлена в другую сторону.
Далее:
