Пример решения задачи по определению реакции шарнира и опоры однородного стержня весом Q, закрепленного шарнирно и свободно опирающегося на опору, на который действует пара сил с заданным моментом.
Задача
Однородный стержень AB (рисунок 1) весом Q = 20 Н в точке A закреплен шарнирно, а в точке C свободно опирается на опору. На стержень AB действует пара сил с моментом M = 5 Нм, а к концу стержня B привязана веревка, перекинутая через блок D, на конце которой висит груз весом P = 5√2 Н.
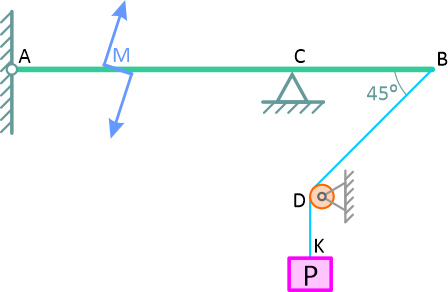
Определить реакции шарнира A и опоры C, если AC= 2BC= 40 см, ∠ABL= 45°.
Другие примеры решений >
Помощь с решением задач >
Решение
Реакция Rc опоры C направлена перпендикулярно к стержню AB. Направление реакции RA шарнира A неизвестно; поэтому раскладываем эту реакцию на две составляющие xA и yA, направленные по осям координат, причем ось Ax направлена вдоль стержня AB, а ось Ay перпендикулярна к нему.
Реакция веревки BD приложена к стержню в точке B и направлена вдоль веревки. Так как натяжение веревки BLK во всех ее точках одинаково, то реакция веревки T равна по величине весу груза P, т.е. T=P.
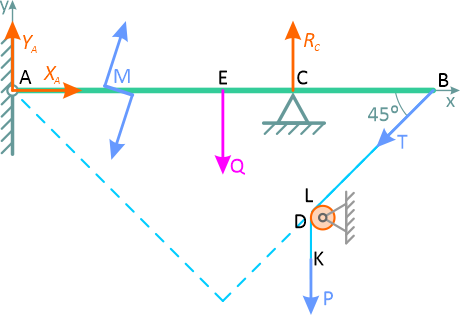
Составим три уравнения равновесия, приравнивая нулю сумму проекций всех сил на координатные оси и сумму моментов этих сил относительно начала координат:
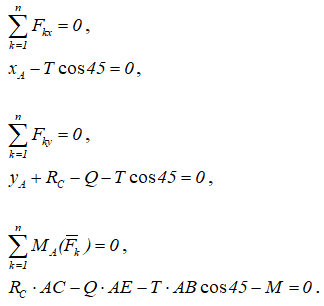
Правила знаков для сил и моментов.
Из первого уравнения находим
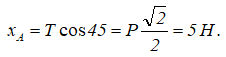
Из третьего уравнения, в котором
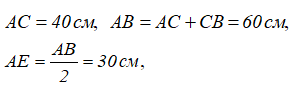
находим
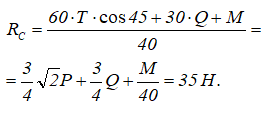
Подставив это значение во второе уравнение, получим
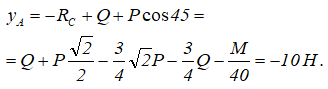
Здесь знак «минус» указывает на то, что в действительности реакция YA направлена в противоположную сторону, т.е. вниз.
