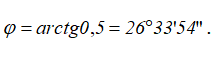Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.

Задача

Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t³ (s в метрах, t в секундах).

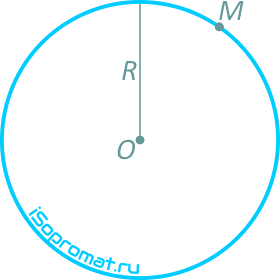
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t₁, когда скорость будет равна 6 м/с (рисунок 1.6).

Другие примеры решений >
Помощь с решением задач >

Решение

Дифференцируя s по времени, находим модуль вектора скорости точки

Другие видео

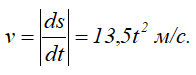
Скорость точки направлена по касательной к траектории (окружности), т.е. перпендикулярно линии радиуса.

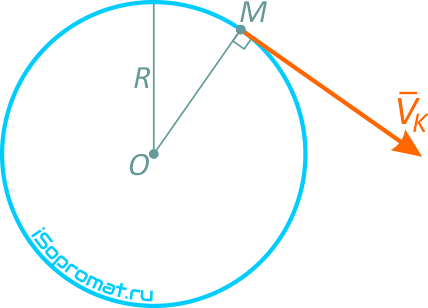
Подставляя в предыдущее выражение значение скорости, получим 6=13,5t₁², откуда находим

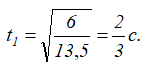
Касательное ускорение для любого момента времени равно

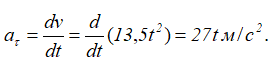
При t=t₁=2/3 с

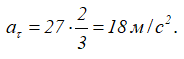
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно

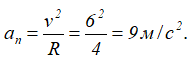
Модуль вектора полного ускорения точки равен

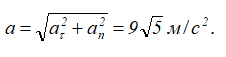
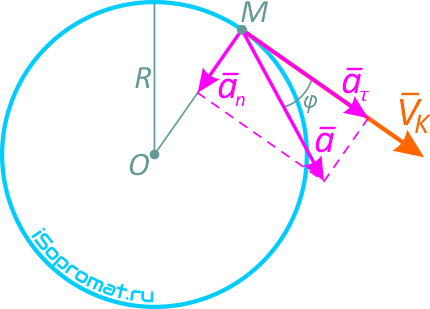
Направление нормального, касательного и полного ускорений точки

Угол между вектором полного ускорения и вектором скорости определим следующим образом:

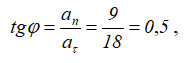
отсюда

Другие примеры решения задач >