Пример решения задачи по определению в заданный момент времени скорости и ускорения точки обода колеса и груза, движущегося равноускоренно из состояния покоя.

Задача

Груз A, подвешенный на нити AB, намотанной на колесо, опускается равноускоренно из состояния покоя, приводя во вращение колесо (рисунок 1.9). За первые 3 секунды колесо совершает 9 оборотов.

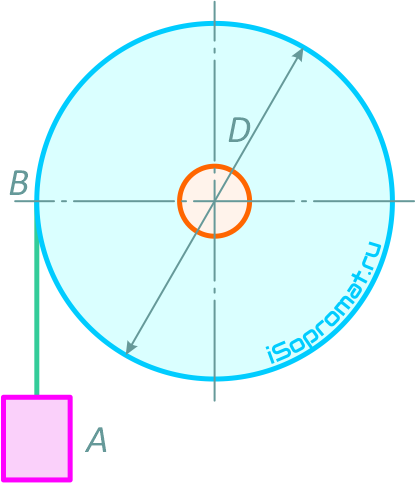
Определить в конце 5-й секунды скорость и ускорение точки обода колеса, а также груза A, если диаметр колеса D=30см.

Другие примеры решений >
Помощь с решением задач >

Решение

Колесо вращается равноускоренно согласно уравнению:

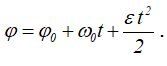
При этом угловая скорость ω = ω₀ + εt.

Примем начальные условия: φ₀= 0 и ω₀= 0, тогда имеем

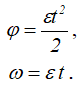
Определим угловое ускорение:

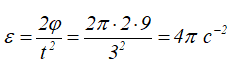
Угловая скорость колеса в конце 5-й секунды

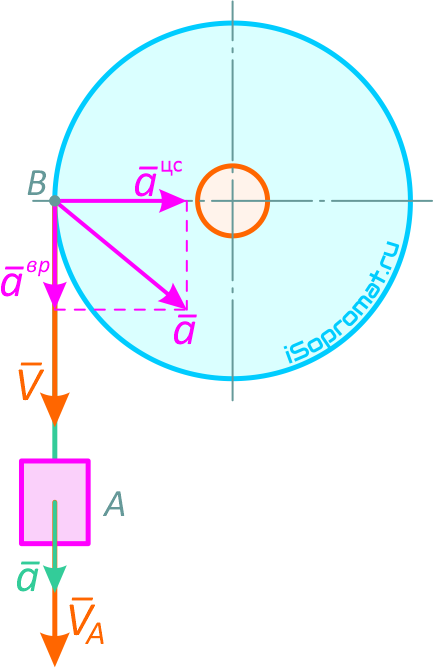
Определим модули вращательной скорости, вращательного и центростремительного ускорений точки обода колеса в тот же момент времени:

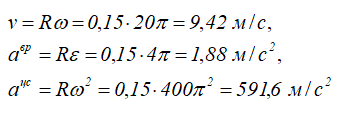
Модуль полного ускорения точки обода колеса

Скорость груза равна скорости точки обода колеса

Ускорение груза равно вращательному ускорению точки обода

Другие примеры решения задач >