Рассмотрим известные методы графического дифференцирования и интегрирования:
Методы графического дифференцирования
Существует три метода графического дифференцирования: метод касательных, метод хорд и метод приращений.
Метод касательных
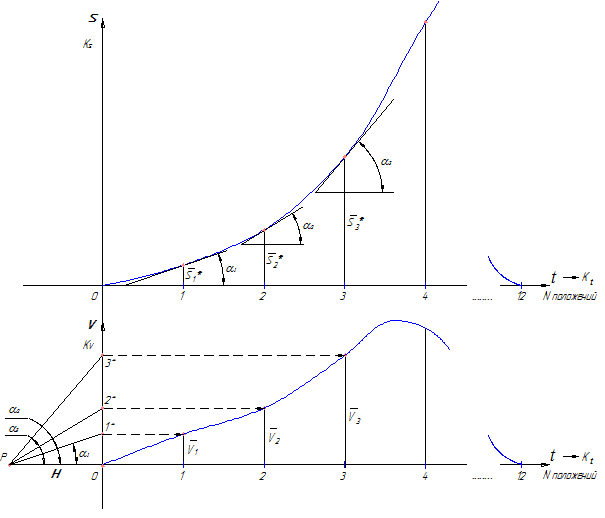
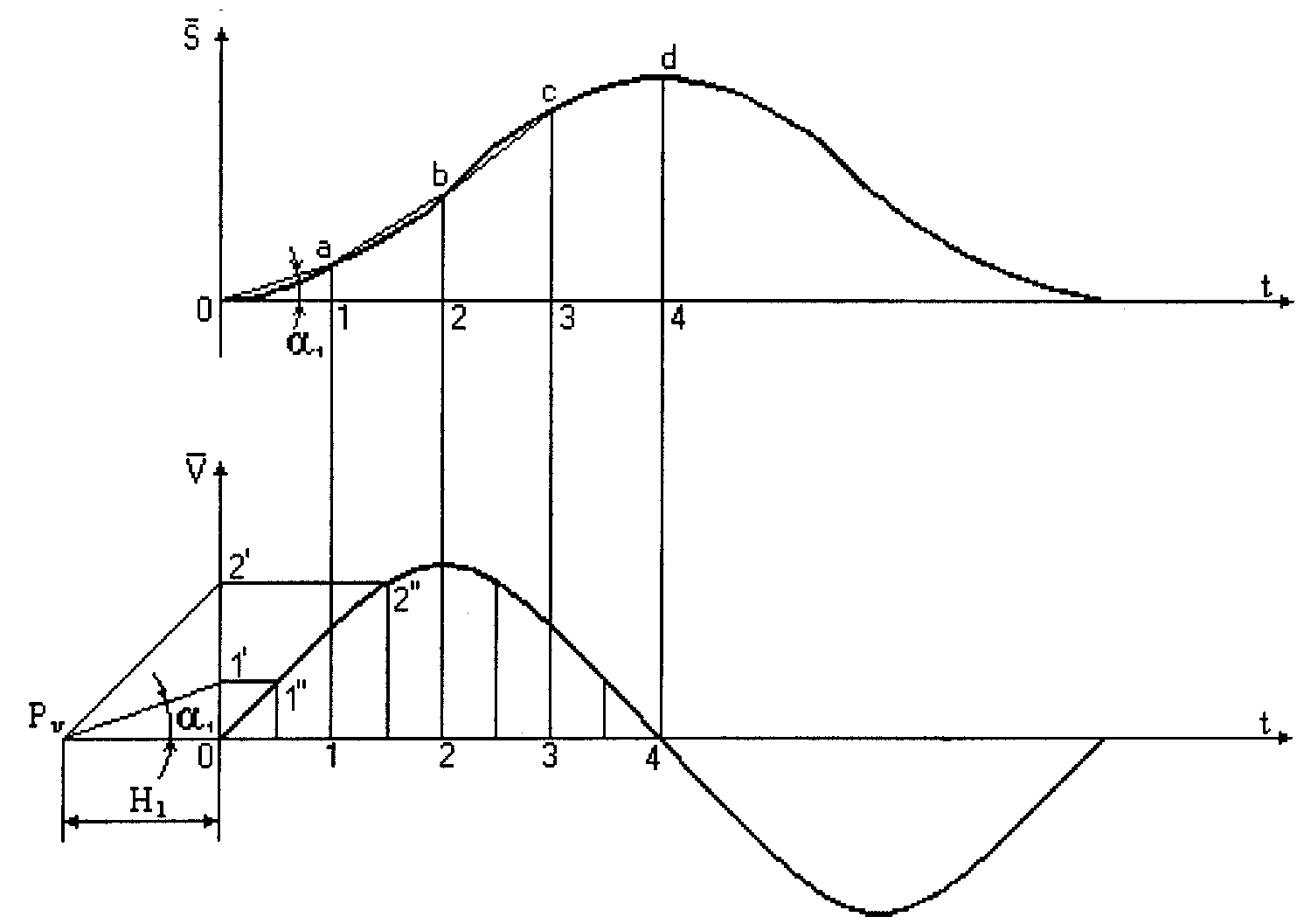
Метод касательных основан на геометрической интерпретации производной. При использовании метода кинематических диаграмм вначале дифференцируется диаграмма перемещений для получения графика (диаграммы) скоростей. Рассмотрим графическое дифференцирование на этом примере.
V = ds/dt, но т.к. аналитическое выражение для перемещений в данном случае отсутствует, то представляем значения перемещений и времени через отрезки на диаграмме перемещений:
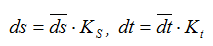
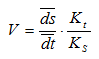
Но отношение бесконечно малого приращения функции к бесконечно малому приращению аргумента на графике представляет собой тангенс угла наклона касательной к данной кривой в рассматриваемой точке, т.е.
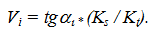
Используя данное обстоятельство, диаграмму скоростей строят в следующем порядке (рисунок 11):
- проводят касательные к диаграмме перемещений в намеченных положениях;
- слева от начала координат на оси абсцисс будущей диаграммы скоростей отмечают полюс P на некотором расстоянии H (которое называется полюсным расстоянием);
- из полюса проводят лучи, параллельные проведенным касательным на диаграмме перемещений. Эти лучи отсекают на оси ординат будущей диаграммы скоростей отрезки
αi
Таким образом, и скорость в i-том положении и отрезки oi* пропорциональны tgαi, а значит отрезки oi* пропорциональны Vi (скорости исследуемого звена в соответствующем положении механизма), т.е. они представляют собой изображение скорости в виде отрезка в некотором масштабе – Vi.
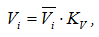
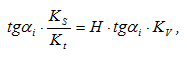
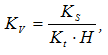
где Kv – масштаб диаграммы скоростей по оси ординат в (м/с)/мм.
Далее отрезки oi* переносят в соответствующие положения, отмеченные на оси абсцисс, и, соединив концы отрезков плавной кривой, получают диаграмму скоростей исследуемого звена. Аналогично строится диаграмма ускорений. При этом масштаб ускорений
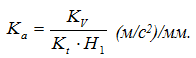
Теоретически метод касательных самый точный из графических методов дифференцирования, т.к. дает значение мгновенной скорости (ускорения) именно в том положении, в котором проведена касательная.
Однако из-за трудности точного проведения касательных (и сама дифференцируемая кривая, построенная по точкам, имеет отклонения от ее теоретической функции), практическая точность этого метода весьма низкая, поэтому он используется редко (обычно когда надо проанализировать характер движения звена без получения конкретных численных результатов).
Метод хорд
При графическом дифференцировании методом хорд последовательность действий точно такая же, что и при методе касательных, но вместо касательных к дифференцируемому графику в конкретных положениях проводят хорды на выделенных участках. В этом случае
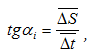
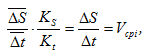
т.е. тангенс угла наклона хорды пропорционален средней скорости на выделенном участке, поэтому отрезки 0i* с оси ординат надо переносить на середины соответствующих участков (считая, что средняя скорость примерно совпадает с мгновенной скоростью посередине выделенного участка). По полученным точкам строят диаграмму скоростей (см. рисунок 12).
Аналогично, дифференцируя диаграмму скоростей, получают диаграмму ускорений. Масштабы всех диаграмм определяют точно так же, как и при использовании метода касательных.
Изначально в методе хорд имеется неточность, связанная с тем, что на самом деле средняя скорость на участке не обязательно совпадает с мгновенной скоростью на его середине. Однако практическая точность его значительно выше, чем при использовании метода касательных, т.к. хорду по двум точкам провести легко с достаточно высокой степенью точности.
Метод тем точнее, чем ближе хорда к дифференцируемой кривой, поэтому делением кривой на более мелкие участки, можно добиться достаточной для практики точности. Поэтому метод хорд применяется значительно чаще, чем метод касательных.
Метод приращений
Метод приращений является частным случаем метода хорд, когда полюсное расстояние принимается равным выделенным участкам на оси абсцисс (при этом все участки должны иметь одинаковую величину H=Δt). В этом случае приращение перемещений на выделенном участке представляет собой среднюю скорость на данном участке в некотором масштабе
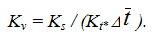
Аналогично дифференцируется диаграмма скоростей для получения диаграммы ускорений. Метод удобен тем, что не надо проводить никаких вспомогательных линий, дифференцирование осуществляется очень быстро. Однако при повторном дифференцировании (дифференцировании диаграммы скоростей для получения диаграммы ускорений) приращения уменьшаются и точность результатов резко снижается (получается большая относительная погрешность).
Методы графического интегрирования
При анализе и, особенно, при синтезе механизмов может быть графически задана функция изменения скорости звена, а необходимо иметь функцию перемещения (или необходимо определить функцию изменения скорости при заданной графически функции ускорения). В этом случае можно воспользоваться методами графического интегрирования.
Применяется два метода графического интегрирования – метод площадей и метод хорд.
Графическое интегрирование методом площадей
Этот метод основан на геометрической интерпретации (физическом смысле) интеграла. Рассмотрим данный метод на примере интегрирования диаграммы скоростей. В результате интегрирования необходимо построить диаграмму перемещений.
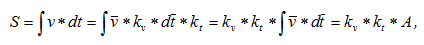
где А – площадь под кривой скорости на выделенном участке (что соответствует физическому смыслу интеграла).
Для интегрирования методом площадей выделяют на оси абсцисс N положений (в пределах одного цикла). Определяют площадь А1 (в мм2) под графиком скорости на участке 0-1, площадь А2 – на участке 1-2, площадь А3 – на участке 2-3 и т.д.
Умножив эти площади на масштаб скоростей и масштаб времени диаграммы скоростей, получают истинные перемещения на выделенных участках, по которым определяют общие перемещения в каждом положении исследуемого звена в расчете от нулевого положения:
S1-2 = Kv ∙ Kt ∙ A2;
S2-3 = Kv ∙ Kt ∙ A3; и т.д.
S2 = S1 + S1-2;
S3 = S2 + S2-3; и т.д.
После определения всех перемещений задают масштаб Ks, в котором строят диаграмму перемещений.
Графическое интегрирование методом хорд
Данный метод основан на том, что интегрирование есть процесс обратный дифференцированию. Поэтому при этом методе производятся все те же действия, что и при дифференцировании методом хорд, только в обратном порядке:
- делят интегрируемую кривую на ряд участков;
- находят среднее значение функции на каждом участке (приближенно можно принимать за среднее значение функции посередине данного участка);
- сносят эти средние значения на ось ординат интегрируемой диаграммы;
- слева от начала координат на оси абсцисс отмечают полюс Р на некотором полюсном расстоянии H;
- соединяют полюс Р с отмеченными на оси ординат точками, характеризующими средние значения интегрируемой функции на выделенных участках. Полученные лучи характеризуют направления хорд на соответствующих участках искомой функции;
- из начала координат проводят хорду на первом участке, параллельную первому лучу;
из конца первой хорды на втором участке проводят хорду, параллельную второму лучу и т.д.
В результате, после построения всех хорд, формируется ломаная кривая, по вершинам которой надо провести плавную кривую.
При интегрировании диаграммы скоростей полученная кривая будет представлять собой диаграмму перемещений (соответственно, при интегрировании диаграммы ускорений, получается диаграмма скоростей). Масштабы полученных диаграмм определяются из зависимостей, выведенных для графического дифференцирования:
Графический метод как алгоритм решения на ЭВМ >
Курсовой проект по ТММ >
