Рассмотрим две гипотезы определения сил трения действующих в пятах машин и механизмов:
Первая гипотеза
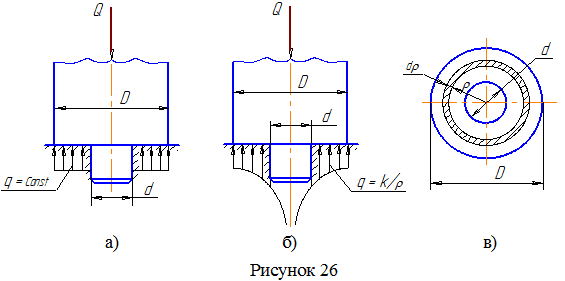
Так как в данном случае опорная поверхность является плоскостью, то постоянное удельное давление (рисунок 26а) определяется простым делением осевого усилия на площадь опорного кольца:
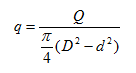
Выделим кольцевой элемент поверхности толщиной dρ на расстоянии ρ от центра пяты (рисунок 26в).
Элементарная нормальная реакция, действующая на этот элемент, определяется умножением удельного давления на его площадь:
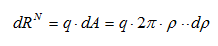
Определим элементарную силу трения и момент от этой силы трения:
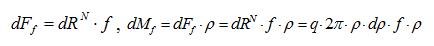
Проинтегрировав по всей опорной поверхности, получим общий момент трения:
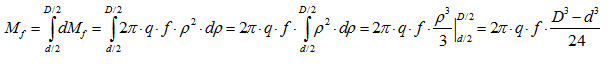
Подставив значение q, окончательно получаем:
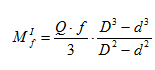
Вторая гипотеза
Как показывает практика, по истечении времени происходит равномерный износ опорной поверхности пяты, т.е. произведение удельного давления на относительную скорость величина постоянная:
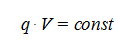
В данном случае скорость в разных точках контактной поверхности различна:
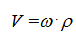
Но так как для вала угловая скорость едина, то износ будет пропорционален произведению q∙ρ другими словами это произведение является некоторой константой k:
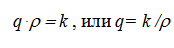
Таким образом, эпюра удельного давления представляет собой гиперболическую зависимость (рисунок 26б). В результате износа поверхности удельное давление перераспределяется таким образом, что при приближении к оси вращения вала оно резко увеличивается (теоретически увеличиваясь до бесконечности в центре опорной поверхности). Именно поэтому сплошные пяты в технике практически не применяются.
Дальнейшее решение ведется аналогично решению по первой гипотезе. В результате получается следующая зависимость для определения момента от сил трения на опорной поверхности пяты:
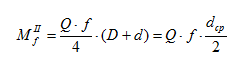
В полученном виде сложно сравнивать гипотезы между собой. Поэтому для оценки результатов рассматривают сплошные пяты (d=0):
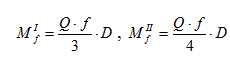
Сравнение показывает, что приработкой поверхностей пяты достигается эффект, аналогичный тому, который имеет место в цапфах – величина сил трения уменьшается на 20…25%.
