Рассмотрим определение составляющих силы трения тела движущегося вверх по наклонной плоскости под действием силы.

В технике для выигрыша в силе часто используется наклонная плоскость. При этом снижается коэффициент полезного действия из-за наличия силы трения между поверхностями.

Рассмотрим общий случай движения тела, нагруженного вертикальной силой Q, вверх по наклонной плоскости под действием силы F, направленной под углом δ к направлению движения. Угол наклона плоскости α (рисунок 21).

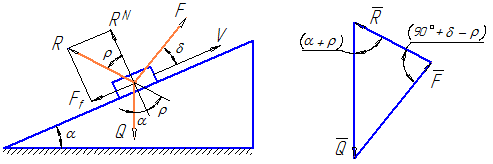
Заменим силу трения и нормальную реакцию результирующей реакцией R. Тогда рассматриваемое тело находится под действием трех сходящихся сил: R, Q и F. Равномерное движение – это равновесное состояние, поэтому при равномерном движении векторная сумма этих сил равна нулю:

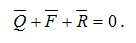
На рисунке 21 приведен векторный треугольник, построенный на основании этой векторной суммы. Из приведенного треугольника по теореме синусов легко определяется зависимость между силами Q и F:

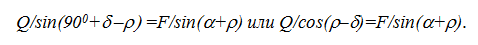
Отсюда общее условие движения (не только равномерного) тела вверх по наклонной плоскости имеет следующий вид:

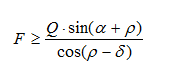
Интерес представляет частный случай, когда движущая сила направлена горизонтально (рисунок 22).

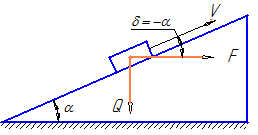
Этот случай описывает работу винтовой пары. Он получается подстановкой в общую формулу значения угла δ = —α.

В результате условие движения тела вверх по наклонной плоскости под действием горизонтальной силы описывается следующим выражением:

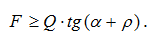
Учет формы направляющих, приведенный коэффициент трения >
Курсовой проект по ТММ >