Теорема о движении центра масс механической системы гласит: центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему.
Выделим условно из механической системы (рисунок 1.1) некоторую материальную точку Mj(mj), на которую будут действовать две силы:
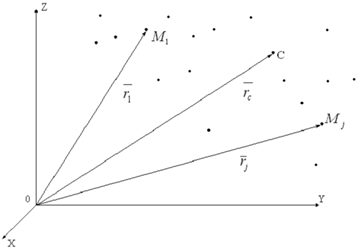
Fji – равнодействующая всех внутренних сил системы;
Fje – равнодействующая всех внешних сил системы.
Рассматривая выделенную точку как свободную, запишем для нее дифференциальное уравнение в векторной форме:
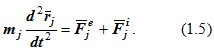
Составим аналогичным образом уравнения (1.5) для всех точек системы (j = 1,2,3,…,n) и формально их просуммируем:
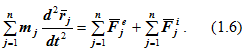
Рассмотрим суммы, стоящие в правой части равенства (1.6):
∑Fji = Ri – главный вектор всех внутренних сил механической системы, который всегда равен нулю (по свойству внутренних сил);
∑Fje = Re – главный вектор всех внешних сил, действующих на механическую систему.
Преобразуем левую часть равенства (1.6):
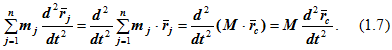
В результате уравнение (1.6) принимает вид
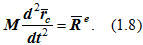
Таким образом, теорема формулируется так: центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему.
Проецируя векторное равенство (1.8) на неподвижные оси декартовых координат, получаем три дифференциальных уравнения движения центра масс:
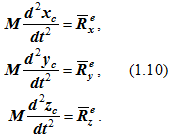
Рассмотрим следствия из теоремы о движении центра масс, вытекающие из формул (1.8) и (1.10):
- если главный вектор внешних сил, действующих на механическую систему, равен нулю, т.е. Re = ∑Fje = 0, то ac= 0 или Vc= const. При этом, если в начальный момент центр масс механической системы был в покое (Vc= 0), то и в дальнейшем центр масс остается неподвижным (rc= const);
- если проекция на какую-либо ось (например на ось Ox) главного вектора внешних сил, действующих на механическую систему, равна нулю, т.е. Rxe = ∑Xje = 0, то acx = 0 или Vcx = const, т.е. имеем закон сохранения проекции скорости центра масс: если проекция главного вектора (алгебраическая сумма проекций) всех действующих на механическую систему внешних сил на какую-либо неподвижную ось равна нулю, то проекция скорости центра масс на эту же ось остается постоянной.
В частности, если в начальный момент Vcx = 0, то и в последующие моменты Vcx = 0 и, следовательно, xc = const, т.е. центр масс системы в этом случае вдоль оси Ox не перемещается.
Примеры решения задач >
Теорема об изменении количества движения материальной точки >
