Пример решения задачи по определению силы сопротивления воздуха свободно падающей тяжелой материальной точке, движущейся по заданному закону.
Задача
Тяжелая материальная точка массой m падает в воздухе, двигаясь по закону
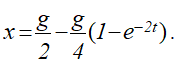
Требуется определить силу сопротивления воздуха.
Решение
Изобразим на рисунке движущуюся точку в произвольный момент времени. Линию, вдоль которой происходит движение, примем за ось Ох, V – скорость точки.
Покажем все действующие на точку силы: G – сила тяжести; Fc – сила сопротивления воздуха (рисунок 2).
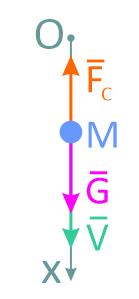
Запишем уравнение второго закона динамики применительно к данной задаче:
![]()
где a – ускорение движущейся точки.
В нашем случае
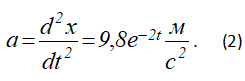
Скорость падения точки
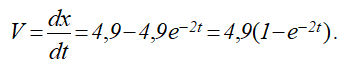
В проекции на ось Ох, уравнение (1) запишется в виде
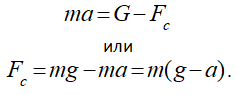
С учетом (2) из последнего выражения получим
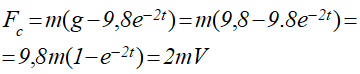
Сила сопротивления получена со знаком «+», что подтверждает правильность ее направления на рисунке.
В задаче по заданному закону движения точки найдена одна из сил, действующих на точку, т.е. решена первая задача динамики.
Далее: