Примеры решения задач и РГР теоретической, инженерной и технической механики по разделам кинематика, статика и динамика, с оформлением графических построений и пояснениями выполняемых действий.

Примеры решения задач по кинематике

Примеры решения задач по разделу «Кинематика» на расчет скоростей, ускорений, траекторий и других кинематических параметров движения точек и твердых тел при различных способах задания движения.

Расчет угловой скорости и радиуса диска

Задача

Точка, лежащая на ободе равномерно вращающегося диска движется со скоростью v=1,6 м/с и нормальным ускорением a_n=8 м/с².

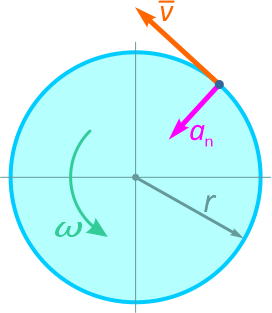
Требуется определить радиус диска r и величину его угловой скорости ω.

Пример решения

Радиус диска определяется по формуле радиуса кривизны траектории движения точки

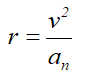
где
v – скорость точки;
a_n – её нормальное ускорение.

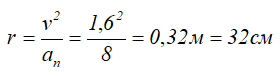
Далее, зная радиус диска, рассчитаем его угловую скорость, которая определяется отношением полной скорости точки к расстоянию от оси вращения диска до самой точки

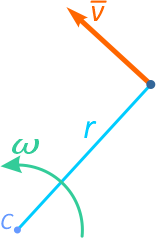
в данном случае, это радиус r окружности обода диска.

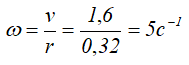
Ответ: Радиус диска r=32 см, угловая скорость составляет ω = 5 радиан в секунду.

Помощь с решением

Далее показаны другие примеры решения задач кинематики (теоретическая, инженерная и техническая механика) по соответствующим подразделам.

Кинематика точки

Примеры расчетов скоростей, нормальных, тангенциальных и абсолютных ускорений точек:

1. Положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, радиус кривизны траектории
2. Траектория движения точки, скорость и ускорение, путь, пройденный точкой
3. Модуль полного ускорения и угол с вектором скорости
4. Параметры движения точки
5. Вид траектории, скорость точки, полное, касательное, нормальное ускорения и радиус кривизны траектории
6. Угол между вектором ускорения и радиусом
7. Расчет скорости и ускорения точки кривошипа

Другие видео

Кинематика твердого тела

Расчеты кинематических параметров движения твердых тел:

1. Сколько оборотов сделает колесо
2. Скорость и ускорение точки обода и груза
3. Угловая скорость вала
4. Скорость точки на ободе диска, её ускорение и угол между вектором ускорения и радиусом диска
5. Скорость и ускорение точки

Плоскопараллельное движение твердого тела

Примеры расчетов скорости и ускорения точек при плоскопараллельном движении твердого тела (ППД):

1. Пример 1
2. Пример 2
3. Пример 3
4. Пример 4
5. Расчет ускорения точки

Сложное движение точки

Примеры решения задач по определению абсолютной скорости и абсолютного ускорения точки при сложном движении:

1. Пример 1
2. Пример 2
3. Пример 3

Сферическое движение

Пример расчетов при сферическом движении:

1. Угловая скорость и угловое ускорение, скорости и ускорения точек тела.

Примеры решения задач по статике

Примеры решения задач по темам статики: расчеты реакций связей и опор при равновесии тел и составных конструкций под действием систем сил, определение усилий в стержнях и координат центров тяжести сложных плоских фигур и объемных тел.

Порядок решения задач на равновесие системы сил

Плоская система сил

1. Определение модуля и направления равнодействующей системы сходящихся сил
2. Составление уравнений суммы моментов сил относительно точки
3. Определение усилий в стержнях
4. Натяжение троса и реакция опоры
5. Опорные реакции невесомой конструкции
6. Опорные реакции в скользящей заделке
7. Определение реакции шарнира и опоры
8. Определение реакций связей аналитическим и графическим способом
9. Определение реакций стержней треугольной системы, удерживающей два груза
10. Определение реакций опор балки, когда сила приложена под углом
11. Определение опорных реакций для разных способов нагружения

Равновесие составных конструкций под действием плоской системы сил

1. Давление в шарнире и реакции в бискользящей заделке
2. Реакции в скользящей заделке
3. Определение реакций в шарнирах
4. Расчет реакций опор и шарнира

Равновесие твердого тела при наличии трения

1. Расчет веса груза необходимого для равновесия тела
2. Определение коэффициента трения обеспечивающего равновесие
3. Расчет угла наклона плоскости при котором цилиндр начнет скатываться
4. Равновесие тела на шероховатой наклонной плоскости
5. Расчет силы для удержания тела при наличии силы трения

Расчет пространственной системы сил

1. Расчет веса противовеса и реакций шарниров
2. Определение величины груза для равновесия и реакции подшипников
3. Определение реакций подшипников пространственно нагруженного вала
4. Реакции опор пространственной системы
5. Натяжение бесконечного ремня
6. Расчет усилия в стержне опоры

Определение координат центра тяжести

Расчет координат положения центра тяжести:

1. Пространственной фигуры
2. Сложной несимметричной фигуры
3. Тонкой однородной симметричной пластинки (плоской фигуры)
4. Сложного сечения
5. Объемного тела

Другие видео
Другие решения задач статики

Помощь с решением

Примеры решения задач по динамике

Примеры решения задач на расчет скоростей, ускорений и других параметров точек, твердых тел и механических систем при их движении с учетом заданных сил.

Движение точки

1. Расчет силы сопротивления воздуха
2. Определение закона движения точки
3. Определение уравнений движения точки
4. Определение закона относительного движения
5. Импульс сил действующих на точку
6. Время необходимое для увеличения скорости в n раз

Движение механической системы

1. Расчет скорости тела в заданный момент
2. Расчет ускорения груза и натяжения нитей
3. Определение обобщенных сил механической системы
4. Определение горизонтального перемещения
5. Горизонтальное движение корпуса двигателя
6. Расчет угловой скорости барабана
7. Угловая скорость системы
8. Определение тормозного пути
9. Угол отклонения стержня от вертикали
10. Закон изменения скорости
11. Определение уравнения колебаний

Расчеты на удар

1. Определение средней ударной силы
2. Расчет среднего сопротивления грунта
3. Угловая скорость после удара
4. Коэффициент полезного действия при ударе

Определение параметров

1. Проекции главного вектора реакций
2. Угол образуемый скоростью с линией действия силы
3. Расчет угловой скорости кривошипа
4. Реакция гладкой горизонтальной поверхности
5. Определение величины момента уравновешивающего силу
6. Определение реакции опоры с помощью принципа возможных перемещений
7. Определение обобщенной силы
8. Определение ускорения треугольной призмы
9. Определение углового ускорения

Другие решения задач динамики

Помощь с решением