Эвольвентное зацепление зубчатых колес удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, допускает отклонение межосевого расстояния зубчатых передач и точно стандартизируется.
Подавляющее большинство зубчатых передач, применяемых в технике, имеет зубчатые колеса с эвольвентным профилем.
Эвольвента как кривая для формирования профиля зуба была предложена Л. Эйлером. Она обладает значительными преимуществами перед другими кривыми, применяемыми для этой цели, – удовлетворяет основному закону зацепления, обеспечивает постоянство передаточного отношения, нечувствительна к неточностям межосевого расстояния (что облегчает сборку), наиболее проста и технологична в изготовлении, легко стандартизируется (что особенно важно для такого распространенного вида механизмов как зубчатые передачи).
На следующем видео показан пример эвольвентного зацепления зубчатых колес
Эвольвента – это траектория движения точки, принадлежащей прямой, перекатывающейся без скольжения по окружности. Данная прямая называется производящей прямой, а окружность, по которой она перекатывается – основной окружностью (рисунок 38 а).
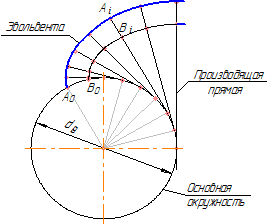
Эвольвента обладает следующими свойствами, которые используются в теории зацепления:
- форма эвольвенты определяется радиусом основной окружности;
- нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;
- эвольвенты одной и той же основной окружности являются эквидистантными (равноотстоящими друг от друга) кривыми.
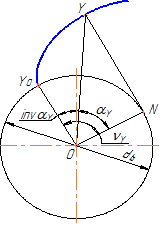
Положение любой точки на эвольвенте может быть однозначно охарактеризовано диаметром окружности, на которой она расположена, а также характерными для эвольвенты углами: углом развернутости (обозначается ν), углом профиля (α), эвольвентным углом – invα (рисунок 38 б). На рисунке 38 б показаны эти углы для произвольно выбранной на эвольвенте точки Y, поэтому они имеют соответствующий индекс:
- νY – угол развернутости эвольвенты до точки у;
- αY – угол профиля в точке Y;
- invαY – эвольвентный угол в точке Y (на окружности диаметра dY ).
То есть индекс показывает, на какой окружности находится рассматриваемая точка эвольвенты, поэтому для характерных окружностей используются индексы, приведенные выше.
Например: αa1 – угол профиля эвольвенты в точке, лежащей на окружности вершин первого колеса;
invα – эвольвентный угол в точке эвольвенты, находящейся на делительной окружности колеса и т.д.
Рассмотрим свойства эвольвенты. Первое свойство имеет строгое математическое доказательство, однако в рамках данного короткого курса оно не приводится.
Так как при формировании эвольвенты производящая прямая перекатывается по основной окружности без скольжения, то в данный момент времени она вращается вокруг точки N (N – мгновенный центр скоростей), описывая бесконечно малую дугу окружности, которая и определяет кривизну эвольвенты в данной точке. Т.е. отрезок NY – это радиус кривизны эвольвенты в точке Y (NY=ρY).
Но отрезок NY в точности равен дуге NY0 (это та же дуга только вытянутая в прямую линию). Таким образом, имеем:
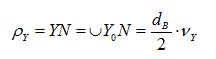
Чем больше радиус основной окружности, тем больше радиус кривизны эвольвенты в любой ее точке (то есть форма эвольвенты действительно определяется величиной радиуса основной окружности).
Второе свойство также легко просматривается. Так как N – мгновенный центр скоростей, то скорость точки Y перпендикулярна радиусу NY. Но скорость точки, движущейся по криволинейной траектории, направлена по касательной к этой траектории – в данном случае по касательной к эвольвенте в точке Y.
Перпендикуляр к касательной – есть нормаль, поэтому прямая YN с одной стороны является нормалью к эвольвенте в точке Y, с другой стороны является касательной к основной окружности (как производящая прямая, перекатывающаяся по основной окружности).
То, что точка N является центром кривизны эвольвенты в точке Y, показано при рассмотрении первого свойства. Запишем некоторые зависимости, которые используются в дальнейшем при изучении геометрии эвольвентного зацепления (получаются из рассмотрения рисунка 38 б):
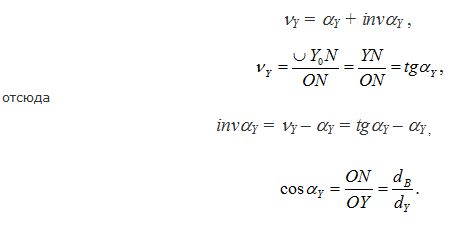
Третье свойство эвольвенты очевидно из рисунка 38а. Действительно, если на производящей прямой взять две точки (А и В), то они будут описывать две совершенно одинаковых эвольвенты, причем, как бы не перемещалась производящая прямая, расстояние между этими точками не изменяется (AiBi = Const). Т.е. действительно это эквидистантные (равноотстоящие друг от друга) кривые. Но, самое важное, что это расстояние AiBi равно расстоянию между этими эвольвентами, измеренному по дуге основной окружности:
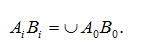
Признаком того, что два криволинейных профиля касаются (а не пересекаются), является наличие у них в точке контакта общей нормали. В связи с этим контакт двух эвольвентных профилей происходит на общей касательной к основным окружностям N1N2 (рисунок 39), которая одновременно будет являться общей нормалью к этим профилям в точке их касания в любой момент времени (на основании второго свойства эвольвенты).
Геометрическое место точек контакта профилей, которое они занимают в процессе работы пары зубьев, называется линией зацепления. Таким образом, в эвольвентной передаче линией зацепления является прямая N1N2 (общая касательная к основным окружностям).
На рисунке 39 а показано зацепление двух эвольвентных профилей в разные моменты времени. В обоих положениях прямая N1N2 является общей нормалью к этим касающимся профилям и проходит через полюс зацепления W (мгновенный центр относительного вращения).
Это, с одной стороны показывает, что эвольвентные профили удовлетворяют основному закону зацепления, с другой стороны обеспечивают постоянство передаточного отношения, т.к. полюс зацепления не меняет своего положения в процессе работы пары (отношение O2W/O1W остается постянным).
С изменением межосевого расстояния будет меняться только положение линии зацепления, но вся картина зацепления останется такой же, т.е. по-прежнему будет сохраняться основной закон зацепления, величина и постоянство передаточного отношения. Это очень важное свойство эвольвентного зацепления, т.к. позволяет вписывать передачу в разные межосевые расстояния, что особенно важно при проектировании коробок скоростей, планетарных и дифференциальных механизмов.
Передача оказывается малочувствительной к неточностям межосевого расстояния, что позволяет снизить требования к точности сборки.
Угол между линией зацепления и общей касательной к начальным окружностям в полюсе называется углом зацепления. Угол зацепления, угол профиля на начальной окружности первого колеса и угол профиля на начальной окружности второго колеса равны между собой (αw1=αw2=αw), поэтому все они обозначаются одинаково – αw (без числового индекса – см. рисунок 39 а).
Отрезок N1N2 называется теоретической линией зацепления. На этом участке происходит нормальная работа двух неограниченных эвольвент.
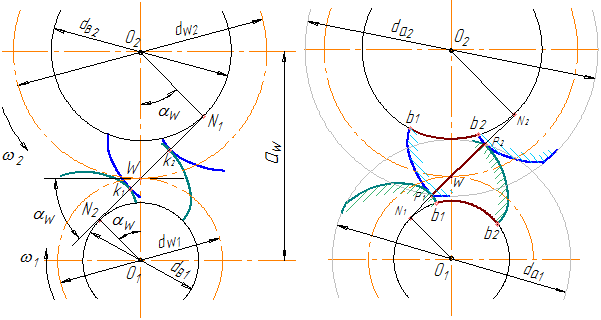
В реальной передаче эвольвенты ограничены («обрезаны») окружностями вершин, поэтому вся работа пары происходит на участке линии зацепления P1P2, заключенном между окружностями вершин (рисунок 39б).
Отрезок P1P2 называется рабочей (активной) частью линии зацепления (иногда называют просто «рабочая линия зацепления», или «активная линия зацепления»). На рисунке 39б показано два положения одной и той же пары: в начале зацепления (зуб ведомого колеса работает своей вершиной, зуб ведущего колеса – нижней рабочей точкой профиля Р1), и в конце зацепления (зуб ведущего колеса работает своей вершиной и в следующий момент выйдет из зацепления, зуб ведомого колеса работает своей нижней рабочей точкой профиля Р2).
Примечание: здесь термин «нижняя» или «верхняя» точка относится к положению точек относительно основной окружности, независимо от того, как эти точки располагаются одна относительно другой в пространстве. Из двух рассматриваемых точек профиля «нижней» будет та, которая располагается ближе к основной окружности.
При увеличении радиуса основной окружности до бесконечности радиус кривизны эвольвенты в любой ее точке также становится бесконечно большим, т.е. основная окружность и эвольвента превращаются в прямые линии. Эвольвентное зубчатое колесо превращается в зубчатую рейку с прямолинейным профилем зуба.
Таким образом, рейка с прямолинейным профилем зуба представляет собой частный случай эвольвентного зубчатого колеса и обладает всеми его свойствами, т.е. может работать с любым эвольвентным колесом (при одном и том же модуле) без нарушения основного закона зацепления. При этом вращательное движение колеса преобразуется в поступательное движение рейки или поступательное движение рейки преобразуется во вращательное движение колеса с соблюдением постоянства передаточного отношения.
Т.к. зубчатая рейка с прямолинейным профилем зуба с одной стороны имеет простые формы и легко задать размеры ее элементов, с другой стороны представляет собой эвольвентное зубчатое колесо, то ее параметры положены в основу стандартизации эвольвентных зубчатых колес. Стандартная зубчатая рейка называется исходным контуром (рисунок 40а).
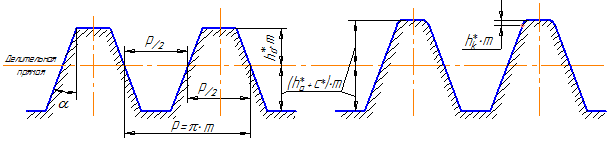
Имеется несколько стандартов на исходные контуры, учитывающие специфику некоторых видов передач (мелкомодульных, конических и т.д.). В основном используются параметры, определенные ГОСТ 13 755 – 81.
В соответствии с этим стандартом исходный контур имеет следующие параметры:
- α = 200 – угол профиля исходного контура (основной параметр, определяющий ряд эвольвент, используемых для зубчатых передач в соответствии с этим стандартом, поэтому часто в конструкторской практике говорят, что у нас в стране используется «двадцатиградусная» эвольвента);
- ha*= 1 – коэффициент высоты головки зуба;
- c*= 0,25 – коэффициент радиального зазора (по другим стандартам в зависимости от модуля и типа инструмента с* может быть равен 0,2; 0,3; 0,35);
Приведенные коэффициенты являются безразмерными величинами. Абсолютное значение какого-либо размера получается умножением соответствующего коэффициента на модуль (Например: высота головки зуба ha=ha*∙m; величина радиального зазора c = c*∙m и т. д.).
Таким образом, форма зуба остается постоянной, а абсолютные размеры определяются модулем (т.е. модуль является как бы коэффициентом пропорциональности).
По высоте зуб исходного контура делится на головку и ножку. Это деление осуществляется делительной прямой. Делительная прямая рейки – это прямая, на которой толщина зуба равна ширине впадины (рисунок 40б).
Высота ножки зуба несколько больше головки для обеспечения радиального зазора между вершинами зубьев одного колеса и окружностью впадин другого после сборки передачи.
Стандартные параметры исходного контура на эвольвентное колесо «переносятся» через делительную окружность (на делительной окружности шаг равен стандартному шагу исходного контура p=π ∙ m, угол профиля равен углу профиля исходного контура α = 200).
Далее: