Для составления дифференциального уравнения вращательного движения твердого тела вокруг неподвижной оси воспользуемся теоремой об изменении момента количества движения (кинетического момента) механической системы относительно оси (3.10):

Пусть на твердое тело, имеющее неподвижную ось вращения z (рисунок 3.4), действует система заданных внешних активных сил (F₁, F₂, F₃,…, F_n), определяющих угловую скорость ω и угловое ускорение ε этого тела в его вращательном движении вокруг оси z. Одновременно на это же тело действуют силы реакции R_A подпятника и R_B радиального подшипника.

Определяем правую часть уравнения (3.11):

Поскольку

то

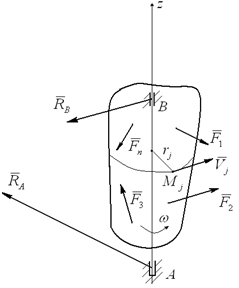
Найдем момент количества движения (кинетический момент) K_z вращающегося твердого тела. Для этого выделим точку M_j тела на расстоянии r_j от оси вращения и имеющую скорость V_j=ω∙r_j. Очевидно, что

Тогда момент количества движения (кинетический момент) всего вращающегося тела будет:

где ∑m_j ∙ r_j²= J_z.

Следовательно, окончательно будем иметь

Подставляя в уравнение (3.11) выражение (3.12), получаем

Уравнение (3.13) представляет собой дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

Поскольку dω/dt = ε, имеем

Полученное выражение (3.14) показывает, что осевой момент инерции J_z тела следует рассматривать как меру инертности твердого тела при его вращательном движении вокруг неподвижной оси.

Примеры решения задач >