В теории удара, явление, при котором за очень малый промежуток времени скорости точек тела изменяются на конечную величину, называют ударом.
Силы, возникающие при таком взаимодействии, называются ударными.
Основные понятия
Ударная сила F достигает значительной величины. Импульс ударной силы называется ударным импульсом и является конечной величиной:
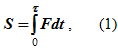
где τ – продолжительность удара (очень малый промежуток времени, в течение которого происходит удар).
В теории удара принимаются следующие основные допущения:
- скорости точек изменяются практически мгновенно на конечную величину;
- импульсами неударных сил пренебрегают;
- точки системы за время удара не перемещаются.
В теории удара применяют теорему об изменении количества движения материальной точки: изменение количества движения материальной точки за время удара равно действующему на эту точку ударному импульсу
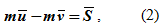
где m – масса точки, ν – скорость точки до удара, u – скорость точки после удара.
При проекции на координатные оси можно получить три скалярных уравнения:
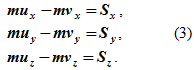
Для механической системы, состоящей из n точек, уравнение (2) можно представить в виде
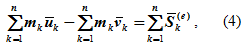
где m – масса k-той точки, νk и uk – скорости k-той точки соответственно до и после удара, Sk(e) – равнодействующая всех внешних ударных импульсов, приложенных к k-той точке.
Теорема об изменении количества движения механической системы при ударе звучит так: изменение количества движения механической системы за время удара равно геометрической сумме всех внешних ударных импульсов, действующих на эту систему.
Уравнение (4) можно записать в виде
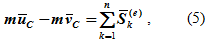
где m – масса всей системы, νc и uc – скорости центров масс системы соответственно в начале и в конце удара.
В проекциях на координатные оси получаем:
mucy — mνcy = ∑Sky(e), (6)
mucz — mνcz = ∑Skz(e).
Теорема об изменении кинетического момента при ударе формулируется следующим образом: изменение кинетического момента механической системы за время удара относительно какого-либо центра равно геометрической сумме моментов всех внешних ударных импульсов, действующих на эту систему относительно того же центра
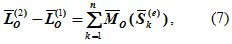
где L0(1) и L0(2) – кинетические моменты системы относительно центра соответственно до и после удара:
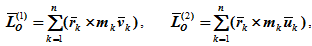
∑M0Sk(e) – сумма моментов внешних ударных импульсов относительно точки O:
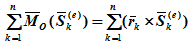
В проекциях на координатные оси уравнение (7) принимает вид:
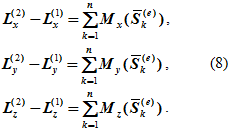
Кинетическая энергия до удара для двух соударяющихся точек или тел, движущихся поступательно, записывается в виде
где v1 и v2 – скорости соударяющихся точек или тел до удара.
Кинетическая энергия точек или тел, движущихся поступательно, после удара равна
где u1 и u2 – скорости точек или тел после удара.
Стадии удара
При ударе двух тел различают две стадии удара. Первая стадия: тела входят в контакт друг с другом и после этого центры масс их продолжают сближаться за счет деформации тел (упругих и пластических). Первая стадия – стадия деформации – заканчивается тогда, когда деформации обоих тел достигают максимального значения.
Вторая стадия – стадия восстановления: упругие свойства тел, если они имели место, заставляют центры масс удаляться друг от друга. В то время как пластические деформации (если они имели место) остаются. Упругие деформации полностью исчезают и тела начинают двигаться порознь.
Степень восстановления формы тел зависит от упругих свойств материалов этих тел и характеризуется соотношением скоростей тел до и после удара.
Ньютоном введен коэффициент восстановления при ударе, величина которого определяется по формуле
где v и u – относительные скорости соударяющихся тел соответственно до и после удара.
Если тело падает с высоты H и после удара о неподвижную поверхность поднимается на высоту h, то коэффициент восстановления равен
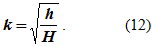
Если удар абсолютно упругий, то соударяющиеся тела полностью восстанавливают свою форму, при этом k = 1. Если удар абсолютно неупругий, то тела на второй стадии не восстанавливают свою форму, при этом k = 0.
Промежуточные значения соответствуют случаям не вполне упругого удара. Случай абсолютно упругого удара (k = 1) имеет лишь теоретическое значение. В зависимости от материала соударяющихся тел коэффициент восстановления имеет различные значения.
