Сферическим движением твердого тела называют такое движение, при котором одна точка тела остается все время неподвижной. Очевидно, траектории всех точек тела при таком движении располагаются на поверхностях сфер.

Для определения положения тела с неподвижной точкой O в каждый момент времени свяжем две системы координат: неподвижную Ox₁y₁z₁ и подвижную Oxyz, жестко связанную с телом, вращающимся вокруг точки O (рисунок 3.1).

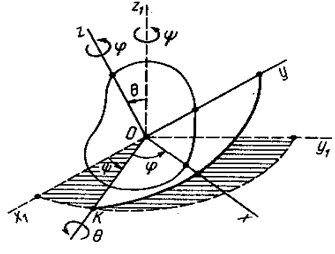
Положение подвижной системы координат относительно неподвижной однозначно определяется тремя углами, называемыми углами Эйлера: ψ — угол прецессии,
θ — угол нутации и
φ — угол собственного вращения.

Линия пересечения подвижной плоскости xOy с неподвижной x₁Oy₁ называется линией узлов OK. Угол прецессии определяет положение линии узлов на неподвижной плоскости x₁Oy₁. Для изменения этого угла тело должно вращаться вокруг оси Oz₁, которую называют осью прецессии.

Угол нутации θ — это угол между осями Oz₁ и Oz. При изменении угла происходит поворот тела вокруг линии узлов, которую также называют осью нутации.

Угол собственного вращения φ — это угол между линией узлов и подвижной осью Ox. При изменении угла φ тело вращается вокруг оси Oz (оси собственного вращения).

Для определения положения тела с одной неподвижной точкой в любой момент времени необходимо задать углы Эйлера как функции времени, т.е.

ψ = ψ(t),

θ = θ(t),

φ = φ(t).   (3.1)

Выражения (3.1) называются уравнениями вращения твердого тела вокруг неподвижной точки.

Примеры решения задач >
Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку >