Лабораторная работа №3. Экспериментальное определение модуля упругости I рода (Юнга)
Цель работы – опытная проверка справедливости закона Гука при растяжении и определение модуля упругости I рода.
Основные сведения
Экспериментальные исследования на растяжение (сжатие) стандартных образцов показывают, что абсолютные удлинения, получающиеся в начальной стадии растяжения (сжатия), остаются прямопропорциональными растягивающей (сжимающей) силе и зависят от первоначальной длины образца l0 и площади поперечного сечения А:
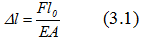
Величина ЕА называется жесткостью стержня при растяжении и сжатии.
Коэффициент Е носит название модуля упругости I рода (используют также название «модуль Юнга» или «модуль продольной упругости«) и является основной физической постоянной, характеризующей упругие свойства (жесткость) материала при линейной деформации.
Чем больше значение Е, тем меньше при прочих равных условиях продольная деформация. Из формулы (3.1) следует, что модуль упругости
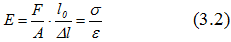
имеет размерность, что и напряжение, — в [Па] или кратных единицах — [кПа], [МПа], а для экспериментального определения его потребуется замерить величины: F, A, l, Δl.
Испытания проводятся на испытательной машине типа Р-5.
Испытывается образец квадратного сечения. Влияние возможной неточности изготовления образца на центральное приложение нагрузки устраняется за счет установки двух тензометров на противоположных продольных гранях образца.
В качестве тензодатчиков используются тензометры Аистова. Среднее удлинение, получаемое из показания двух тензодатчиков, принимают равным удлинению оси образца.
Диапазон нагрузок зависит от состояния и класса точности установки и предела пропорциональности материала образца. Минимальная загрузка зависит от жесткости самой установки (выборка лифтов, затяжка клиньев и т.п.) и определяется опытным путем. Максимальная загрузка рассчитывается по формуле
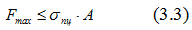
Зная диапазон нагрузок, определяют количество и величину ступеней нагружения ΔF.
Порядок выполнения и обработка результатов
Перед началом выполнения лабораторной работы необходимо ознакомиться с устройством машины Р-5 и рычажным тензометром Аистова.
Образец с закрепленными на нем тензодатчиками устанавливают в захватах машины и приводят в рабочее состояние.
Производят предварительное (минимальное) нагружение образца начальной нагрузкой и при этой нагрузке снимают показания приборов.
Далее нагрузку увеличивают плавно равными ступенями ΔF (5-6 ступеней) и производят соответственно снятие показаний с тензометров.
Доводить нагрузку до очередного значения нужно плавно, не «перескакивая» нужное значение. После осуществления загрузки последней ступени следует разгрузить образец до нагрузки, соответствующей минимальной.
При очередной ступени загрузки результаты опыта заносят в таблицу. Каждому приращению ΔF будет соответствовать приращение ΔП1i и ΔП2i, по которым подсчитывают среднее значение
Истинное значение удлинения образца находим как
где К = 10-3 мм – цена 1 деления тензометра Аистова.
По значениям нагрузки F и суммарному нарастанию удлинения оси образца строят график диаграммы растяжения образца в координатах F : Δl, по которому проверяют линейность зависимости (справедливость закона Гука).
Для среднего приращения нагрузки (ступени нагружения) определяют среднюю продольную абсолютную деформацию
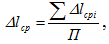
где П – число ступеней нагружения.
Модуль продольной упругости
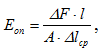
где l – база тензометра Аистова.
Полученное в опыте значение модуля упругости Еоп сравнивают с табличным ЕТ = 2·1011 Па и определяют погрешность опыта.
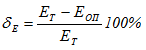
В заключение работы делают выводы.
Контрольные вопросы
- Как формулируется закон Гука для линейного напряженного состояния? Как ограничить верхнюю максимальную нагрузку?
- Каковы границы применения закона Гука?
- Что характеризует модуль упругости Е, от чего он зависит и какова его размерность?
- По какому геометрическому выражению с использованием диаграммы напряжений можно определить Е?
- Почему при определении деформаций растянутого образца используют два тензометра?
Далее: