Законом Гука называют базовую зависимость в механике, устанавливающую взаимосвязь между усилиями и соответствующими им упругими деформациями.
Закон был открыт в 1660 году английским ученым Робертом Гуком.
Проведя серию экспериментов с растяжением и сжатием пружин, Гук заметил, что изменение их длины прямо пропорционально растягивающей (сжимающей) их силе.
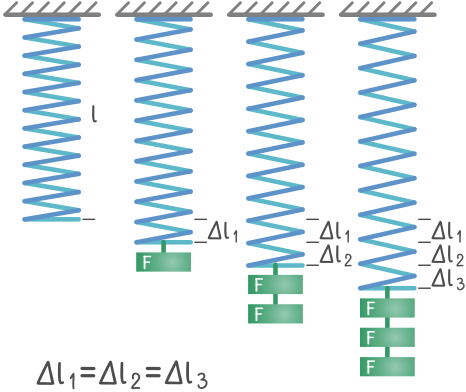
Свои наблюдения он оформил в виде закона: «Какова сила, таково и удлинение».
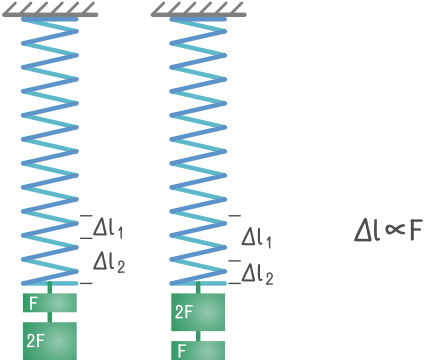
Современная формулировка закона существенно отличается от оригинала и зависит от дисциплины, в которой рассматривается зависимость деформаций от усилий.
Подробнее про закон Гука смотрите в нашем видео:
Закон Гука в физике
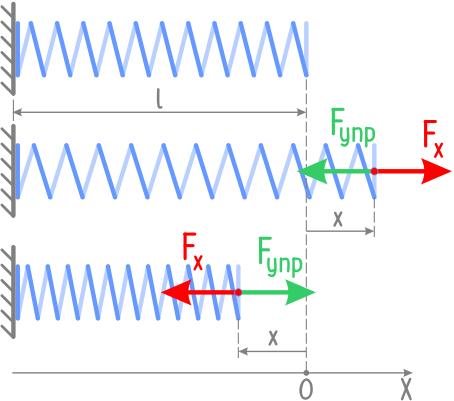
В современных учебниках физики Закон Гука имеет вид:
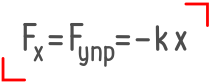
и формулируется следующим образом:
«При малых деформациях сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения его частиц»
Коэффициент k характеризует жесткость образца и зависит от его размеров и материала.
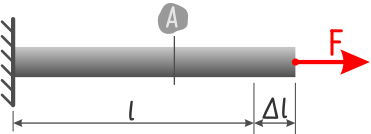
Например, для стержней, работающих на растяжение или сжатие, он может быть рассчитан по формуле: 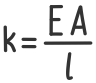 где:
где:
E – Модуль упругости I рода (модуль Юнга);
A – Площадь поперечного сечения бруса;
l – Длина стержня.
Знак минус означает, что силы упругого сопротивления направлены обратно растягивающей силе.
Закон Гука в сопромате
В технической механике и сопротивлении материалов в частности закон Гука гласит: «До определенного момента, называемого пределом пропорциональности, упругие деформации прямо пропорциональны напряжениям».
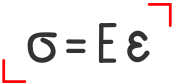
Здесь:
σ — Нормальные напряжения в сечении;
ε — Относительные продольные деформации.
Рассмотрим преобразование физической формы закона к его механическому виду.
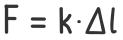
Подставим вместо коэффициента k его выражение
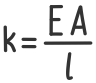
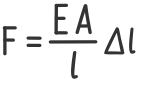
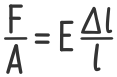
Отношение продольной силы F к площади поперечного сечения A в левой части дает нормальные напряжения в сечении
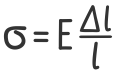
Отношение абсолютных деформаций к начальной длине образца – это относительное изменение его длины
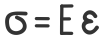
В таком виде закон Гука используется в сопромате и технической механике.
Закон выполняется только для напряжений не превышающих предела пропорциональности.
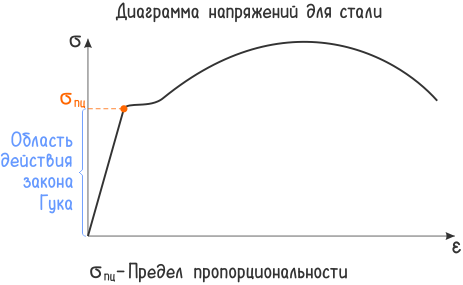
При растяжении и сжатии
При растяжении и сжатии закон Гука можно получить, вернув в его канонический вид геометрические параметры стержня (длину и площадь поперечного сечения), и записав получившееся выражение относительно линейной деформации:
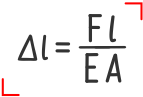
Здесь
Δl- Абсолютная деформация стержня;
F — Продольная сила;
l — Длина стержня до нагружения;
E – Модуль продольной упругости материала;
A – Площадь поперечного сечения стержня.
При изгибе
При изгибе закон устанавливает зависимость между кривизной продольной оси и величиной изгибающего момента в соответствующем сечении балки.
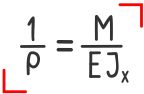
где:
ρ — Радиус кривизны продольной оси балки в данном сечении;
M — Величина соответствующего внутреннего изгибающего момента;
E – Модуль Юнга;
Ix — Осевой момент инерции поперечного сечения балки.
Обобщенный закон Гука
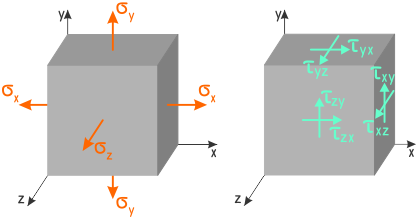
Для общего случая нагружения изотропных материалов, когда напряженное состояние отличается от линейного (одноосного) применяется закон Гука в обобщённом виде.
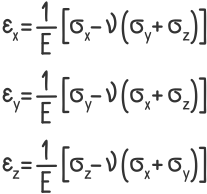
ε — Относительные деформации вдоль соответствующих осей;
ν — Коэффициент Пуассона;
σ — Нормальные напряжения по соответствующим площадкам элемента.
Потому что деформации в поперечных направлениях тоже влияют на изменение продольных размеров.
Для чистого сдвига
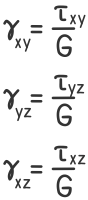
γ — Угловое перемещение соответствующей площадки элемента;
τ — Касательные напряжения;
G — Модуль упругости II рода (модуль сдвига).
Далее:
Теория и примеры решения задач по предметам: