Рассмотрим теорему об ускорении точек при плоскопараллельном движении твердого тела:
При плоском движении ускорения точек определяются согласно следующей теореме:
Из выражения VM=VA+VMA
(или VM=VA + ω
⋅ AM ) путем дифференцирования получаем
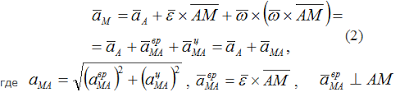
aврMA=ε ⋅ AM — вращательное ускорение точки М при вращении вокруг точки А.
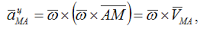
aцMA=ω2⋅ AM — центростремительное ускорение точки М при вращении вокруг точки А.
Центростремительное ускорение a—цMA направлено от точки М к полюсу А.
Численную величину полного ускорения можно определить, спроецировав векторное равенство (2) на выбранные оси координат:
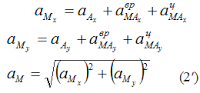
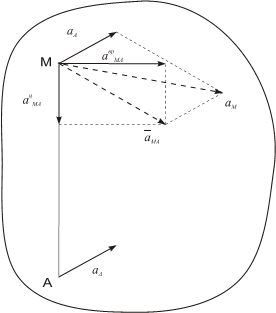
Рис. 1.11
