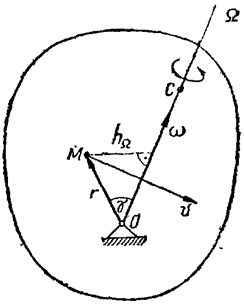
Скорости точек твердого тела, совершающего сферическое движение, в каждый момент времени определяются как их вращательные скорости при вращении вокруг мгновенной оси Ω (рисунок 3).

Рисунок 3

Зная положение мгновенной оси вращения Ω и угловую скорость тела ω, можно определить скорость любой точки тела M как скорость этой точки во вращательном движении вокруг мгновенной оси по известной формуле

где
r — радиус-вектор точки M, проведенный из неподвижной точки O.

Модуль скорости

где h_Ω — расстояние точки от мгновенной оси вращения.

Введем подвижную Oxyz и неподвижную Ox₁y₁z₁ системы координат аналогично рисунку 1.

Для проекций скорости точки на неподвижные и подвижные оси получены формулы Эйлера:

• для неподвижной системы координат
  
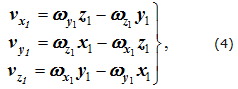
• для подвижной системы координат
  

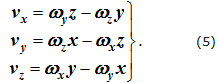
Из этих формул можно получить уравнения мгновенной оси в неподвижной и подвижной системах координат, положив для точек, лежащих на мгновенной оси, все проекции скорости равными нулю.

• Для неподвижной системы координат:
  
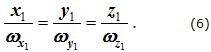
• Для подвижной системы координат:
  

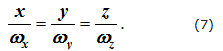
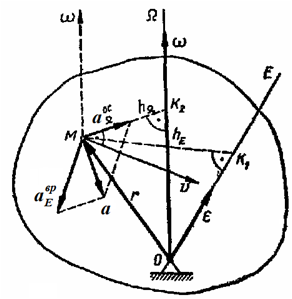
Если положение мгновенной оси Ω уже установлено, то для нахождения угловой скорости сферического движения ω достаточно знать скорость v какой-либо точки M, не лежащей на мгновенной оси (рисунок 3).

Рисунок 4

Тогда, опустив из этой точки перпендикуляр h_Ω на мгновенную ось Ω, получим v = ω × h_Ω, откуда

Для определения ускорения точки твердого тела служит теорема Ривальса: ускорение любой точки твердого тела при сферическом движении определяется как геометрическая сумма ее вращательного и осестремительного ускорений

где

— вращательное ускорение точки,

— осестремительное ускорение точки.

Модули этих ускорений (рисунок 4)

где
h_E — расстояние от точки до оси углового ускорения E,

h_Ω — расстояние от точки до мгновенной оси Ω.

Модуль ускорения точки можно найти как диагональ параллелограмма:

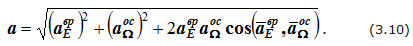
При сферическом движении вектор осестремительного ускорения a_Ω^ос направлен по перпендикуляру, опущенному из точки на мгновенную ось Ω, а вращательное ускорение a_E^вр оказывается перпендикулярно плоскости проходящей через вектор углового ускорения ε и радиус-вектор r.

Направление вращательного ускорения не совпадает с направлением вектора скорости v.

---

Далее: