Траектории точек вращающегося твердого тела представляют собой окружности, поэтому, при определении скорости и ускорения точек удобнее пользоваться естественным способом задания движения (рисунок 15).
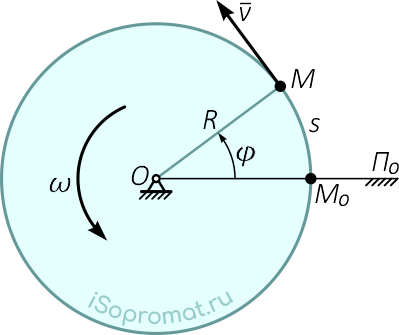
Рисунок 15
Дуговая координата, определяющая положение точки на траектории, связана с углом поворота равенством:
![]()
Отсюда:
![]()
Скорость v точки M
![]()
называют линейной или окружной скоростью.
Окружная скорость всегда направлена по касательной к траектории точки.
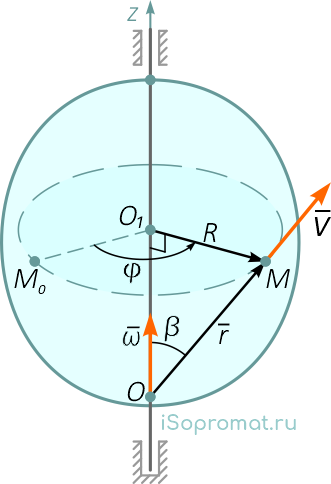
Рисунок 16
Модуль скорости точки вращающегося тела (рисунок 16)
![]()
равен модулю векторного произведения
![]()
Следовательно:
![]()
Это формула Эйлера для определения величины окружной (линейной) скорости точки в векторном виде при вращательном движении твердого тела.
Далее: