При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.
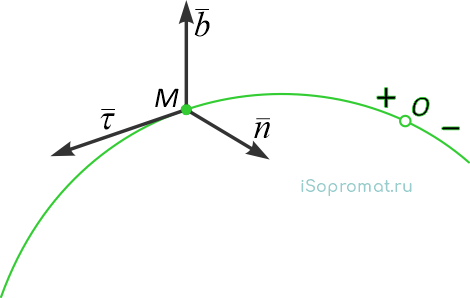
На рисунке 1.4:
τ — орт касательной;
n — орт нормали;
b — орт бинормали.
Единичные орты
![]()
определяют направление соответствующих осей в каждой точке кривой.
Чтобы задать закон движения точки естественным способом необходимо:
- знать траекторию движения;
- установить начало отсчета на этой кривой;
- установить положительное направление движения;
- задать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).
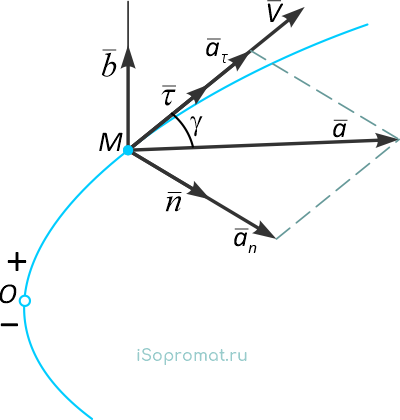
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).
Скорость и ускорение точки при естественном способе задания движения
Скорость точки при естественном способе задания её движения определяется по формулам
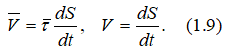
Первая формула определяет величину и направление вектора скорости, вторая формула только величину.
Ускорение определяется как производная от вектора скорости:
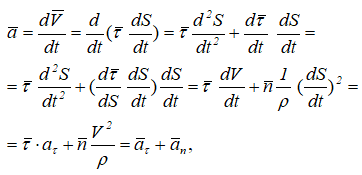
т.е.
![]()
В формуле (1.10)
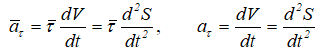
— касательное ускорение. Оно характеризует быстроту изменения величины скорости точки;
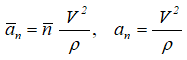
— нормальное ускорение точки. Характеризует быстроту изменения направления вектора скорости;
ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).
Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):
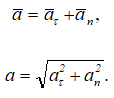
Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному и обратно.
Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.
Например,
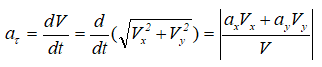
или
![]()
Далее, для естественнго способа задания движения точки, получаем
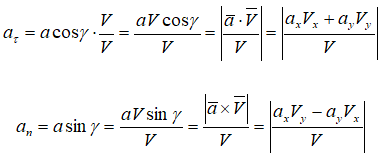
Далее: