В общем случае, моментом силы F относительно точки O является результат векторного произведения радиуса-вектора, проведенного из точки O в точку приложения силы, на вектор этой силы:
![]()
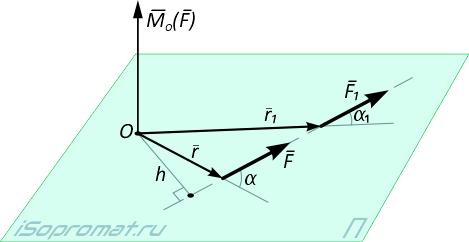
Вектор MO(F) (рисунок 1) перпендикулярен плоскости, в которой лежат радиус-вектор r и вектор силы F, и направлен так, что если смотреть навстречу ему, видно силу, стремящуюся повернуть плоскость П, в которой она лежит, против хода часовой стрелки.
Наш короткий видеоурок с примерами:
Численно момент силы относительно точки равен
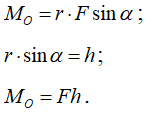
На рисунке 1 видно, что если силу перенести вдоль линии действия в другую точку, то величина и знак момента не изменятся:
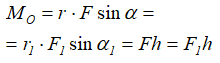
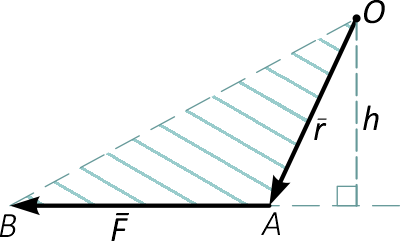
Можно также сказать, что величина момента силы относительно точки равна удвоенной площади треугольника (OAB), основанием которого является сила, а высотой – плечо h (рисунок 2):
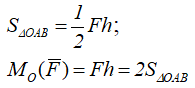
В некоторых случаях для расчета величины момента силы относительно точек удобнее пользоваться теоремой Вариньона.
Пример расчета
К стержню OA длиной 3 м, расположенному под углом α=30° в точке A приложена горизонтальная сила F=50 Н.
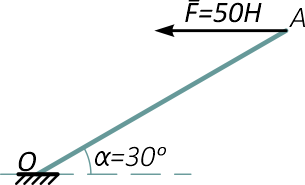
Требуется вычислить момент силы F относительно точки O стержня.
Решение
Определяем плечо силы, проведя нормаль из точки O к линии действия силы F
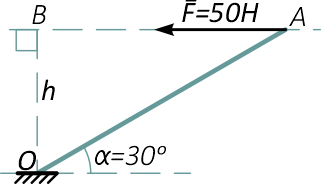
Рассчитаем длину плеча OB
![]()
Тогда величина момента силы относительно точки O
![]()
По правилу знаков, момент в данном случае положителен.
Далее: