Пример решения задачи по определению усилий в стержне и опорных реакций плиты заданного веса, закрепленной с помощью шарнирно-неподвижной опоры и цилиндрическим шарниром.
Задача
Однородная прямоугольная плита ABCD весом G закреплена в точке A с помощью шарнирно-неподвижной опоры, в точке B цилиндрическим шарниром, в точке D шарнирно скреплена невесомым стержнем DE (рисунок 2.14, а).
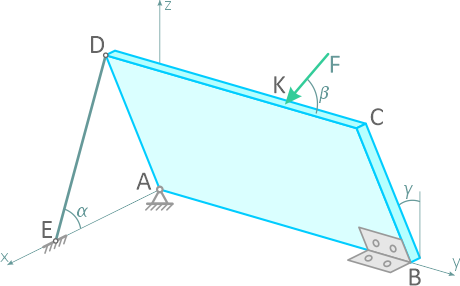
Плита составляет с вертикальной плоскостью угол γ, в точке K на нее действует сила F, находящаяся в вертикальной плоскости. Определить опорные реакции и усилие в стержне DE.
Другие примеры решений >
Помощь с решением задач >
Решение
Короткое видео про реакции в разных типах связей:
В задаче необходимо рассмотреть равновесие плиты, к которой приложены силы G и F и реакции связей: RD, XA, YA, ZA, XB, ZB (рисунок 2.14, б).
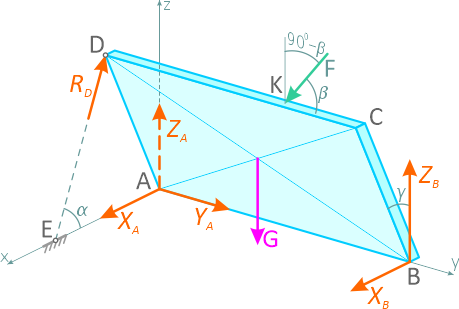
Чтобы яснее представить расположение сил, на рисунке 2.15 покажем проекции плиты и действующих сил на соответствующие плоскости.
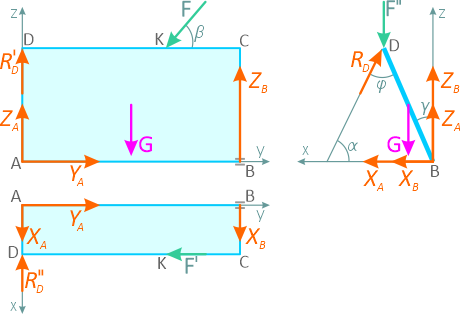
Уравнения равновесия для конструкции:
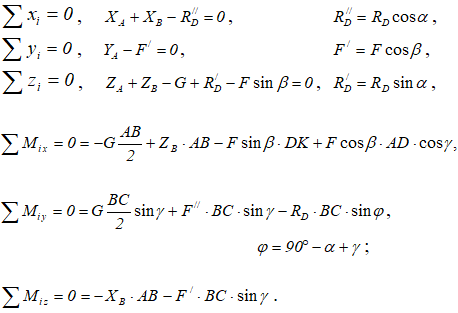
Решая систему из шести уравнений, определяем реакции опор и усилие RD в стержне DE.
