Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.
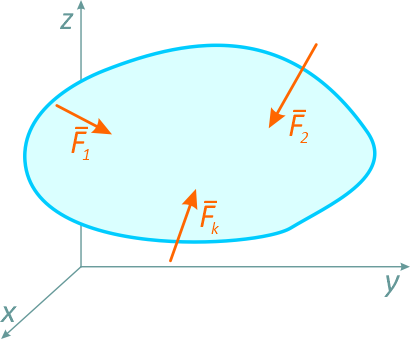
Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).
Отсюда вытекает условие равновесия произвольной пространственной системы сил.
В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю
![]()
В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю
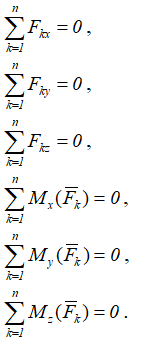
Эти условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин, например, реакций связей.
Чтобы задача была статически определимой, число неизвестных должно быть не более шести.
В частности, для системы параллельных сил условиями равновесия являются следующие равенства
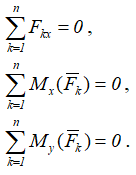
Далее: