Пример решения задачи на построение эпюр внутренних поперечных сил Qy и изгибающих моментов Mx для стальной балки на двух шарнирных опорах, нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
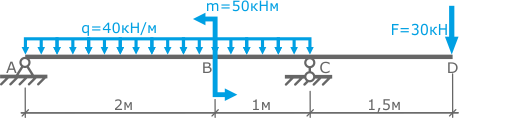
Для заданной двухопорной балки, нагруженной силой F, моментом M и равномерно распределенной нагрузкой q построить эпюры внутренних поперечных сил Qy и изгибающих моментов Mx.
Другие примеры решений >
Помощь с решением задач >
Решение задачи
Опорные реакции для данной расчетной схемы были определены здесь.
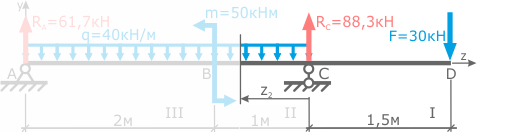
Балка имеет 3 силовых участка. Обозначим их римскими цифрами, например, справа налево.
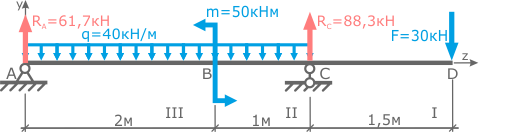
Для расчета внутренних силовых факторов по участкам балки воспользуемся методом сечений.
Расчет значений
Начнем с первого силового участка (CD).
Проведем поперечное сечение в пределах участка, в любом месте между точками C и D.
Данное сечение делит балку на две части (левую и правую). Для определения внутренних факторов можно выбрать любую из них, но лучше выбирать менее нагруженную часть балки. Очевидно это будет ее правая часть.
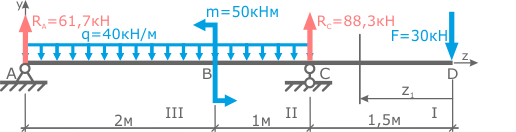
Расстояние от правой границы участка до рассматриваемого сечения обозначим переменной z1, которая может принимать значения от 0 до 1,5 метров (т.е. 0 ≤ z1 ≤ 1,5м).
Подробно, все расчеты значений и построение эпюр Q и M для балки показаны в нашем видеоуроке:
Мысленно отбросим на время всю левую часть балки.
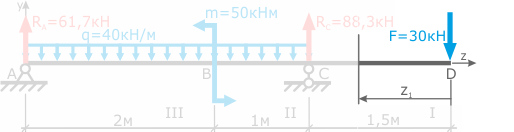
Поперечная сила Q в данном сечении первого участка будет равна сумме всех внешних сил приложенных к рассматриваемой части балки с учетом их знака, т.е.
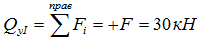
В данном выражении отсутствует переменная z1, что говорит о том, что внутренняя поперечная сила будет одинакова для всех сечений этого участка.
Изгибающий момент M в рассматриваемом сечении определяется как сумма изгибающих моментов от всех внешних нагрузок выбранной части балки.
С учетом правила знаков при изгибе получаем
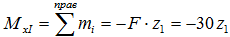
В полученном выражении переменная z1 является плечом момента силы F для данного сечения балки.
Как видно из полученного выражения изгибающий момент по длине участка меняется линейно (т.к. z1 в первой степени), поэтому для построения эпюры на данном участке нам достаточно двух точек.
Этими точками будут значения изгибающего момента на границах I участка, т.е. при z1=0 и при z1=1,5м
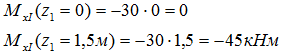
На первом участке внутренние усилия определены.
Переходим на второй силовой участок (BC).
Так же начинаем с того, что проводим сечение в любом месте участка и выбираем рассматриваемую часть балки. Здесь также удобнее рассмотреть правую часть балки.
Расстояние до рассматриваемого сечения от правой границы участка обозначим переменной z2. При этом 0 ≤ z2 ≤ 1м.
Запишем выражения и рассчитаем граничные значения внутренней поперечной силы Q
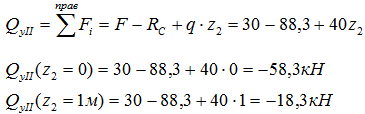
И изгибающего момента M
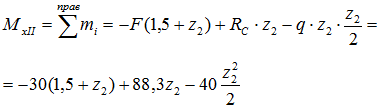
Здесь опорная реакция RC положительна, потому что сжимает верхний слой, а сила F и распределенная нагрузка q отрицательны, т.к. сжимают нижний слой балки.
Как записывается момент распределенной нагрузки показано здесь.
В выражении для MxII переменная во второй степени, поэтому эпюра моментов на втором участке будет иметь вид параболы.
Как известно, для построения параболы необходимо знать положение минимум трех ее точек. Но как будет показано дальше, в некоторых случаях при построении эпюр, параболы можно вычерчивать всего лишь по двум точкам. Рассчитаем их значения:
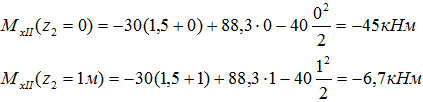
Осталось найти внутренние усилия на III силовом участке (AB).
Рассекаем балку между точками A и B. Выбираем менее нагруженную левую часть. 0 ≤ z3 ≤ 2м – интервал возможных положений сечения относительно левой границы участка.
Записываем выражения для Q и M и вычисляем значения в крайних точках
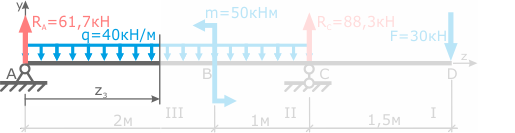
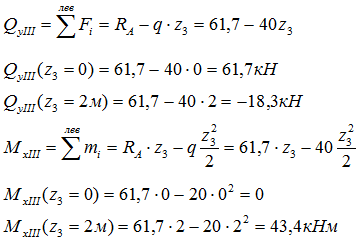
Здесь видно что выражение для QyIII — линейное, а на эпюре Mx на данном участке будет парабола.
По полученным данным строим эпюры.
Построение эпюр
Для построения эпюр рассчитанные значения откладываем от базовой линии на соответствующих участках.
Начинаем с эпюры поперечных сил Q.
На первом участке выражение для Q не зависело от z1 поэтому его значение будет постоянным (QyI=const) по длине участка, т.е. линия эпюры будет параллельна базовой.
На втором участке были получены два значения Q: -58,3 кН при z2=0 и -18,3кН при z2=1м. Переменная z2 откладывалась от правой границы участка, поэтому z2=0 в точке C, соответственно в т. B переменная z2=1м.
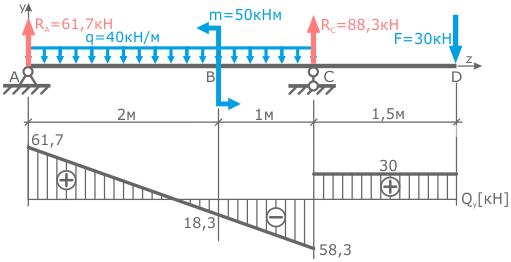
Аналогично откладываются значения Q на третьем участке и значения M на эпюре изгибающих моментов.
Точки на II и III участках эпюры Q и на I участке эпюры M соединяются отрезками, так как распределение внутренних сил и моментов там линейное (переменная z в первой степени).
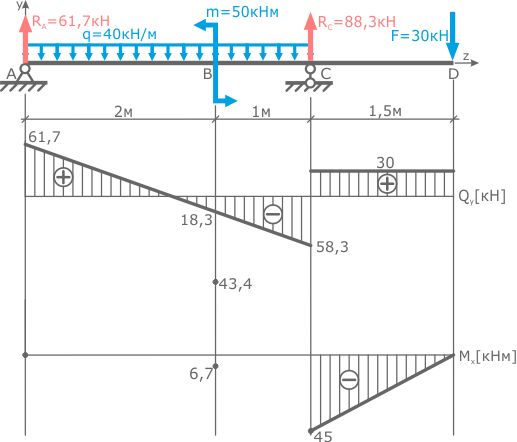
А при соединении точек эпюры M параболами, надо смотреть на эпюру Q.
Дело в том, что эпюра поперечных сил это первая производная эпюры изгибающих моментов. Поэтому в сечениях балки, где Q=0 на эпюре M будет экстремум.
Как видно эпюра Q пересекает нулевую линию только на третьем силовом участке балки. Поэтому, ввиду того что нас интересуют только пиковые значения изгибающих моментов, на втором участке две крайние точки достаточно соединить параболой, не имеющей экстремума, выпуклость которой направлена навстречу распределенной нагрузке.
Для более точного построения линии параболы на данном участке можно найти значения момента для промежуточных положений сечения, например при z2=0,5м.
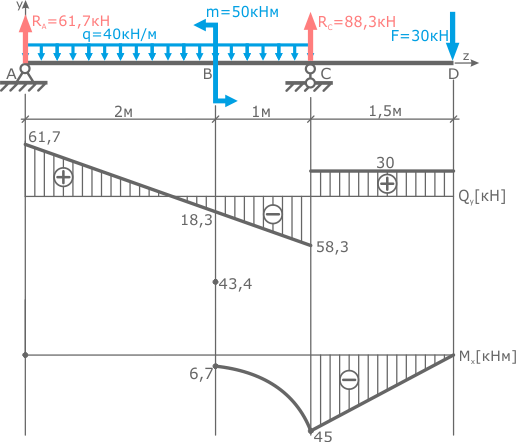
На третьем участке, в сечении, где Q пересекает базовую линию необходимо рассчитать точку экстремума.
Как рассчитывать экстремум эпюры моментов
Для этого выражение для QyIII приравнивается к нулю и рассчитывается значение z3, при котором изгибающий момент на участке принимает экстремальное значение. Его подставляют в выражение для MxIII
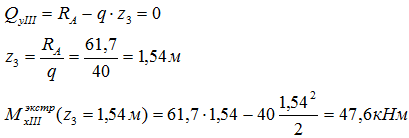
Это значение откладывается на эпюре M под точкой пересечения эпюры Q с базовой линией
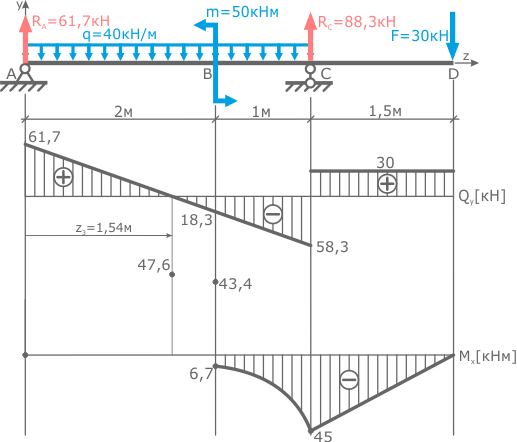
после чего три точки соединяются плавной линией.
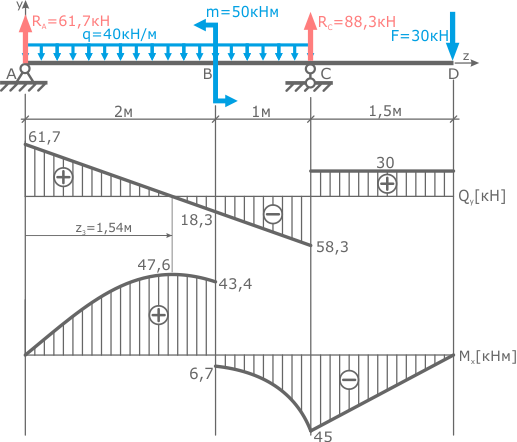
Эпюры внутренних поперечных сил и изгибающих моментов построены.
Проверка эпюр поперечных сил >
и изгибающих моментов >
Расчеты для подбора сечений балки >
Другие примеры решения задач >
