Пример решения задачи по расчету опорных реакций балки, закрепленной на двух шарнирных опорах и нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
Для заданной двухопорной балки с консольной частью, нагруженной комплексом нагрузок: силой F, моментом m и распределенной нагрузкой q, определить величину и направление опорных реакций.
Расчетная схема балки показана на рис.1
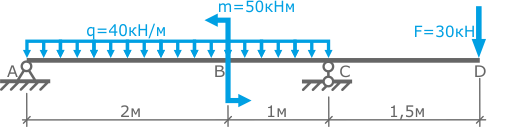
Длина пролета балки 3м. Длина консольной части – 1,5м.
Пример решения
Рекомендуем посмотреть наш видеоурок. В нем мы постарались подробно показать порядок расчета реакций в опорах балки.
Для решения задачи, обозначим характерные точки (сечения) балки (точки A, B, C и D) и определим положение системы координат y-z, выбрав ее начало например в т. A (рис.2)
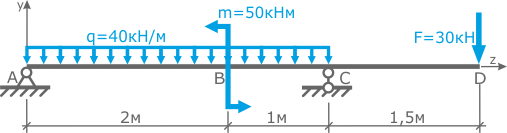
Обе опоры балки являются шарнирными, поэтому в каждой из них будет возникать только сила, обозначим их соответственно RA и RC
Видео про реакции в шарнирных опорах
Пример расчета реакций опор для консольной балки
Так как все заданные нагрузки раположены исключительно в вертикальной плоскости (плоский поперечный изгиб) и не дают проекций на ось z, то опорные реакции будут тоже только вертикальными.
Вообще говоря, реакции в опорах являются такими силами, которые необходимы для удержания балки с приложенными к ней нагрузками, в статичном (неподвижном) состоянии. В данном случае эти силы не позволяют ей вращаться и перемещаться в вертикальной плоскости.
Данная балка является статически определимой, т.к. уравнений равновесия достаточно для определения неизвестных усилий в опорах балки.
Для составления уравнений статики, опорные реакции RA и RC предварительно направляются произвольно, например, вверх (рис.3).
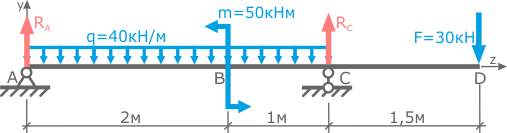
Для определения двух неизвестных реакций потребуется два уравнения.
Запишем уравнения статики:
- Балка не перемещается по вертикали, т.е. сумма проекций всех сил на ось y равна нулю:
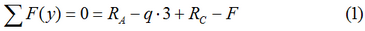 Здесь, по правилу знаков для проекций сил на ось, нагрузки направление которых совпадает с положительным направлением оси y записываются положительными и наоборот.
Здесь, по правилу знаков для проекций сил на ось, нагрузки направление которых совпадает с положительным направлением оси y записываются положительными и наоборот. - Тот факт, что балка не вращается, говорит о том, что сумма моментов относительно любой ее точки тоже равна нулю, т.е.:
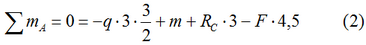 В данном уравнении, согласно правила знаков для моментов, сосредоточенные силы, моменты и распределенные нагрузки стремящиеся повернуть балку против хода часовой стрелки относительно рассматриваемой точки A записываются положительными и наоборот.
В данном уравнении, согласно правила знаков для моментов, сосредоточенные силы, моменты и распределенные нагрузки стремящиеся повернуть балку против хода часовой стрелки относительно рассматриваемой точки A записываются положительными и наоборот.
Как записывается момент распределенной нагрузки показано здесь.
Сила приложенная в точке относительно которой рассматривается сумма моментов в уравнении не участвует, так как плечо момента для нее равно нулю.
Здесь сумму моментов лучше записывать относительно точки расположенной на опоре (например, A), т.к. в этом случае соответствующая реакция RA в уравнении не участвует.
Из выражения (2) определяем RC:
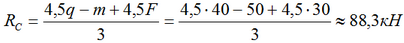
и подставив его в выражение (1) находим RA:
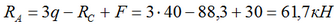
Направление и величина реакций, как правило, необходимы для дальнейших расчетов балки на прочность и жесткость, поэтому во избежание возможных ошибок рекомендуется выполнять проверку найденных значений.
Далее: