При координатном способе задания движения точки в выбранной системе координат задаются координаты движущейся точки как функции от времени.
В прямоугольной декартовой системе координат это будут уравнения:
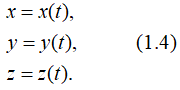
Эти уравнения являются и уравнениями траектории в параметрической форме.
Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.
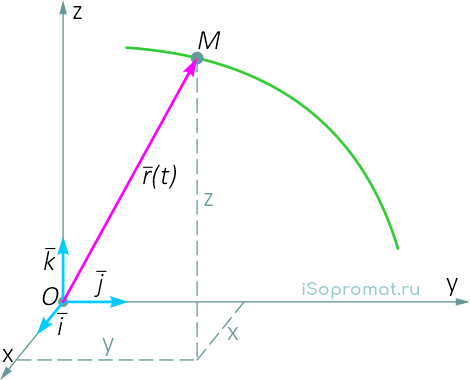
Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):
![]()
Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:
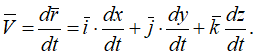
То есть:
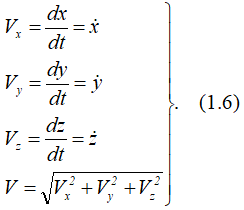
Направление вектора скорости определяется с помощью направляющих косинусов:
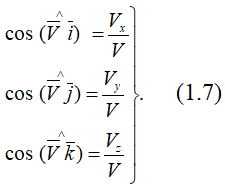
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.
Аналогичны формулы для определения ускорения точки:
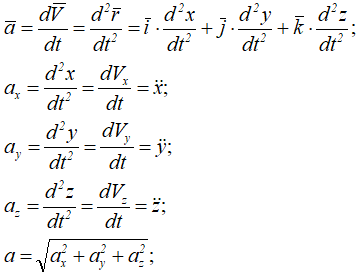
Направляющие косинусы ускорения точки
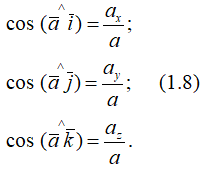
Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных проекций скоростей и ускорений точек на оси декартовой системы координат.
Далее: