Пример решения задачи по определению уравнений колебательных движений движущейся механической системы при известных массе, расстоянии от центра тяжести и моменте инерции.
Задача
Определить уравнения колебаний подпрыгивания и продольной качки головного пассажирского вагона электропоезда, имеющего две тележки (рисунок 4.2), если известно, что масса вагона при нормальном заполнении его пассажирами равна 31500 кг.
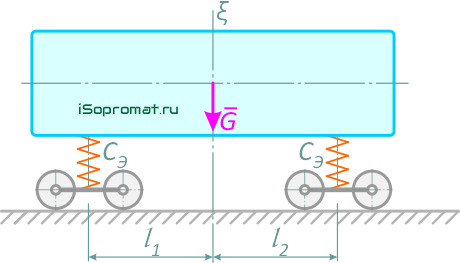
Расстояние от центра тяжести подрессоренной части вагона до вертикальных плоскостей, проведенных через оси тележек, l1=l2=l=6,65 м, момент инерции подрессоренной части – кузова вагона с пассажирами относительно центральной оси Cξ, перпендикулярной к оси пути, JCξ=11,5∙105 кг∙м2, а эквивалентная жесткость двойного рессорного подвешивания каждой тележки Cэ=1580 кН/м.
Другие примеры решений >
Помощь с решением задач >
Решение
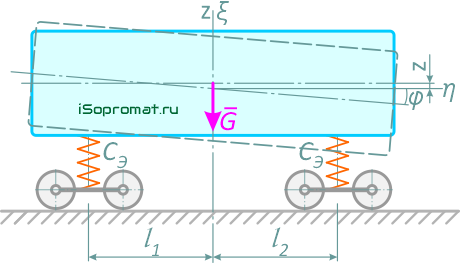
Система имеет две степени свободы, соответственно в качестве обобщенных координат выберем отклонение центра тяжести вагона от положения покоя по вертикали z и поворот оси вагона от горизонтали φ.
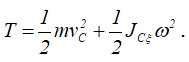
Так как
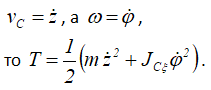
Потенциальную энергию системы найдем как сумму потенциальной энергии подрессоренной части вагона в поле сил тяжести и потенциальной энергии деформированных рессор тележек Π2:
![]()
Здесь
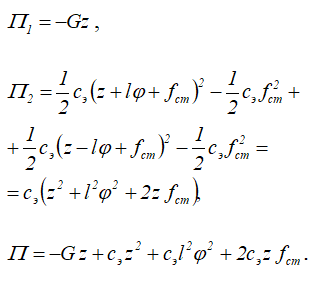
Так как
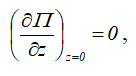
то
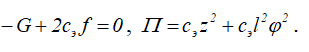
Вычислим производные
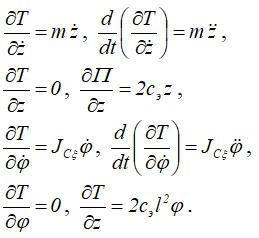
Подставим производные в уравнения
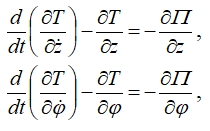
получим
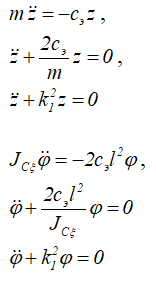
где
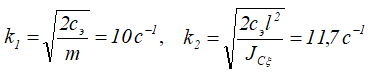
Мы получили две пары независимых линейных дифференциальных уравнений, интегрируя которые найдем уравнения движения:
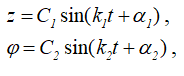
где C1, C2, α1, α2 – постоянные, определяемые из начальных условий.
