Под числом степеней свободы кинематической цепи подразумевается число степеней свободы подвижных звеньев относительно стойки (звена, принятого за неподвижное). Однако сама стойка в реальном пространстве может перемещаться.
Как отмечалось выше, число входных звеньев для превращения кинематической цепи в механизм должно равняться числу степеней свободы этой кинематической цепи.
Например, любое неподвижное тело на Земле имеет нулевую степень свободы, но в Мировом пространстве вместе с Землей оно перемещается, используя все шесть степеней свободы.
Другой пример: кинематическая цепь, положенная в основу поршневого двигателя, имеет одну степень свободы относительно стойки (звена, принятого при исследовании за неподвижное, которое состоит из цилиндра, присоединенного к картеру и раме или корпусу автомобиля, мотоцикла или другой машины), хотя при движении машины сама стойка также перемещается.
Однако, независимо от того движется машина или нет, характер движения звеньев поршневого двигателя относительно стойки остается неизменным.
Введем следующие обозначения:
k – число звеньев кинематической цепи;
p1 – число кинематических пар первого класса в данной цепи;
p2 – число пар второго класса;
p3 – число пар третьего класса;
p4 – число пар четвертого класса;
p5 – число пар пятого класса.
Общее число степеней свободы k свободных звеньев, размещенных в пространстве, равно 6k. В кинематической цепи они соединяются в кинематические пары (т.е. на их относительное движение накладываются связи).
Кроме того, в качестве механизма используется кинематическая цепь, имеющая стойку (звено, принятое за неподвижное). Поэтому число степеней свободы кинематической цепи будет равно общему числу степеней свободы всех звеньев за вычетом связей, накладываемых на их относительное движение:
Число связей, накладываемых всеми парами I класса, равно их числу, т.к. каждая пара первого класса накладывает одну связь на относительное движение звеньев, соединенных в такую пару; число связей, накладываемых всеми парами II класса, равно их удвоенному количеству (каждая пара второго класса накладывает две связи) и т.д.
У звена, принятого за неподвижное, отнимаются все шесть степеней свободы (на стойку накладывается шесть связей). Таким образом:
а сумма всех связей
В результате получается следующая формула для определения числа степеней свободы пространственной кинематической цепи:
Сгруппировав первый и последний члены уравнения, получаем:
или окончательно:
где n – число подвижных звеньев кинематической цепи.
Данное уравнение носит название структурной формулы кинематической цепи общего вида.
Формула была получена впервые ( в несколько ином виде) П.И. Сомовым в 1887 г., и развита А.П. Малышевым в 1923 г. Поэтому ее часто называют формулой Сомова-Малышева. В некоторых учебниках ее называют формулой Малышева – по авторству окончательного варианта.
Примечание: авторы некоторых учебников придают иной смысл индексу при обозначении числа кинематических пар pi , а именно:
p1 – число одноподвижных пар (т.е. кинематических пар, обеспечивающих одну степень свободы в относительном движении),
p2 – число двухподвижных пар и т.д.
То есть индекс в данном случае показывает не число связей, а число степеней свободы и в формуле обозначения p1 и p5 , а также p2 и p4 меняются местами. Поэтому при использовании различных учебников необходимо внимательно следить за интерпретацией автора, т.к., к сожалению, часто разные авторы в одно и то же обозначение вкладывают разный смысл. В результате при одних и тех же обозначениях одни и те же формулы имеют различный вид.
В манипуляторах и промышленных роботах используются разомкнутые (открытые) кинематические цепи. В таких цепях число подвижных звеньев равно общему числу кинематических пар:
т.е.
или окончательно:
Таким образом, число степеней свободы разомкнутой кинематической цепи равно сумме подвижностей (степеней свободы) кинематических пар, входящих в эту цепь. Кроме степеней свободы на качество работы манипуляторов и промышленных роботов большое влияние оказывает их маневренность.
Маневренность – это число степеней свободы манипулятора при неподвижном захвате. Она определяет способность манипулятора (промышленного робота) обходить препятствия и вычисляется по следующей формуле:
где M – маневренность манипулятора.
Как было отмечено выше, значительное число применяемых на практике механизмов являются плоскими механизмами (т.е. в их основе лежат плоские кинематические цепи). Помещение кинематической цепи в плоскость накладывает три общие связи на движение всех звеньев этой цепи, поэтому k свободных звеньев, помещенных в плоскость, имеют в общей сложности 3k степеней свободы.
На плоскости существуют только пары четвертого и пятого классов. На кинематическую пару четвертого класса приходится одна связь (в дополнение к трем общим связям, приходящимся на плоскость); на пару пятого класса приходится две связи; у стойки отнимаются все три степени свободы. Таким образом:
Это есть структурная формула для плоской кинематической цепи.
Эта формула впервые была предложена П.Л. Чебышевым в 1869 г. и ее часто называют формулой Чебышева.
Формула Чебышева (как в прочем и формула Сомова-Малышева) дает абсолютно правильный результат для общего случая кинематической цепи, состоящей из соответствующего числа звеньев и кинематических пар.
Однако конструктор из множества размеров и форм звеньев может подобрать такие, которые обеспечат подвижность цепи при нулевой степени свободы, или обеспечить работоспособность механизма с помощью одного двигателя при числе степеней свободы больше единицы. То есть, как и в большинстве случаев жизни, здесь имеются исключения из правил.
Если кинематическая цепь, имеющая в соответствии с формулой Чебышева нулевую степень свободы, оказывается подвижной, это означает, что в данной цепи имеются пассивные (избыточные) связи. При исследовании механизма в этом случае звенья, создающие пассивные связи, просто удаляются из рассмотрения.
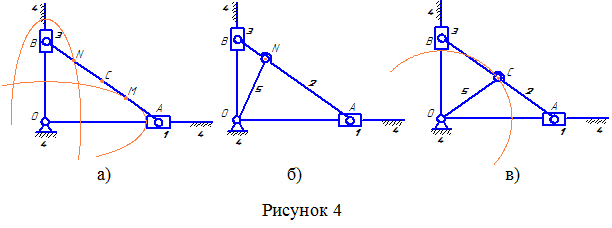
На рисунке 4а показана кинематическая схема механизма эллипсографа (W=3 ∙ 3 – 2 ∙ 4 = 1). Он обладает следующими свойствами: точки A и B движутся поступательно вдоль осей X и Y как принадлежащие ползунам 1 и 3.
При этом точка M описывает эллипс с малой полуосью, равной отрезку AM и расположенной вдоль оси Y, и с большой полуосью BM, расположенной вдоль оси X (т.е. эллипс, вытянутый вдоль оси X); точка N описывает эллипс с малой полуосью BN и с большой полуосью AN, вытянутый вдоль оси Y.
Точка C (середина отрезка AB) описывает «эллипс» с равными полуосями, т.е. окружность. Если некоторое звено 5 присоединить шарнирами к неподвижной точке O (начало координат) и к какой-либо точке на звене AB (например, к точке N – рисунок 4б), то получится неподвижная система (ферма):
Однако, если звено 5 присоединить вторым шарниром к звену AB в точке C (рисунок 4в), то движение точки C, принадлежащей звену 5, и движение точки C, принадлежащей звену AB, становятся согласованными – обе точки движутся по одной и той же траектории (по окружности радиуса OC).
В этом единственном частном случае кинематическая цепь становится подвижной (формула не может «предусмотреть» такой частный случай – она дает результат для общего случая соответствующего сочетания звеньев и кинематических пар). В данном случае звено 5 накладывает пассивную (избыточную) связь и при исследовании механизма это звено можно не учитывать.
Наличие пассивных связей можно установить построением нового положения заданной кинематической цепи с нулевой (или отрицательной) степенью свободы по тем же размерам звеньев. Если цепь строится в других положениях, она имеет пассивные связи. Если же размеры не стыкуются в новом положении, то это действительно неподвижная система – ферма (при отрицательном числе степеней свободы – ферма статически неопределимая).
Лишние степени свободы – если в механизме имеется движение какого-либо звена, не влияющее на движение остальных звеньев этого механизма, то оно дает лишнюю степень свободы.
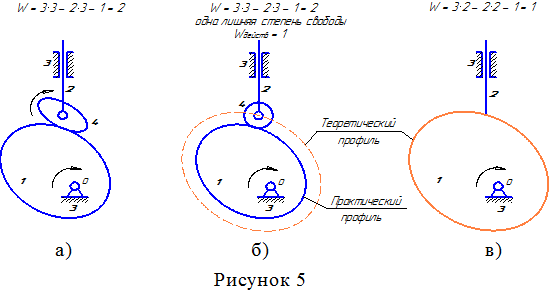
Обычно лишняя степень свободы образуется при наличии круглого ролика. Вращаясь вокруг собственной оси, он не изменяет характера движения остальных звеньев.
На рисунке 5а изображен механизм с некруглым роликом – здесь положение толкателя 2 будет зависеть не только от положения кулачка, но и от положения ролика. То есть механизм действительно имеет две степени свободы. В механизме на рисунке 5б ролик круглый и его угол поворота не влияет на положение толкателя – положение толкателя полностью определяется положением кулачка.
Таким образом, фактически механизм имеет одну действующую степень свободы (вращение ролика вокруг собственной оси дает формально вторую степень свободы, но это движение не оказывает влияния на движение остальных звеньев механизма).
При исследовании механизма удобно избавиться от лишней степени свободы. Для этого надо практический профиль заменить теоретическим – эквидистантным профилем, проходящим через центр ролика, и удалить ролик из рассмотрения (рисунок 5в).
Далее: